解:(1)设直线OM的函数关系式为y=kx,P(a,

)、R(b,

).
则M(b,

),
∴k=

÷b=

.
∴直线OM的函数关系式为y=

x.
(2)∵Q的坐标(a,

),满足y=

x,
∴点Q在直线OM上.
∵四边形PQRM是矩形,
∴SP=SQ=SR=SM=

PR.
∴∠SQR=∠SRQ.
∵PR=2OP,
∴PS=OP=

PR.
∴∠POS=∠PSO.
∵∠PSQ是△SQR的一个外角,
∴∠PSQ=2∠SQR.
∴∠POS=2∠SQR.
∵QR∥OB,
∴∠MOB=∠SQR.
∴∠POS=2∠MOB.
∴∠MOB=

∠AOB.
(3)①先做出钝角的一半,按照上述方法先将此钝角的一半(锐角)三等分,进而做出再做一个角与已做得的角相等即可得到钝角的三等分角.
②先作钝角的邻补角的三等分角,然后再以得到的三等分角作等边三角形可得钝角的三等分角,在钝角内作做出这个角即可.
分析:(1)直线OM是正比例函数,可利用所给的坐标得到M的坐标,代入函数解析式即可;
(2)根据所给的点的坐标得到Q的坐标,看是否符合(1)中的函数解析式;运用矩形的性质,作图过程中的条件,外角与不相邻内角的关系,即可得证;
(3)既然能作出锐角的三等分角,先将此钝角的一半(锐角)三等分,再作钝角的三等分角.
点评:过某个点,这个点的坐标应适合这个函数解析式.注意使用作图过程中利用的条件.

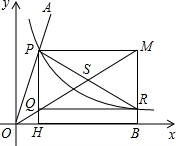
 的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数表达式(用含a,b的代数式表示);
),求直线OM对应的函数表达式(用含a,b的代数式表示); ∠MOB=
∠MOB= ∠AOB;
∠AOB; )、R(b,
)、R(b, ).
). ),
), ÷b=
÷b= .
. x.
x. ),满足y=
),满足y= x,
x, PR.
PR. PR.
PR. ∠AOB.
∠AOB.

 ∠MOB=
∠MOB=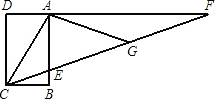 “三等分一个角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的,在探索中,有人曾利用过如下的图形:其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠GFA,你能证明∠ECB=
“三等分一个角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的,在探索中,有人曾利用过如下的图形:其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠GFA,你能证明∠ECB=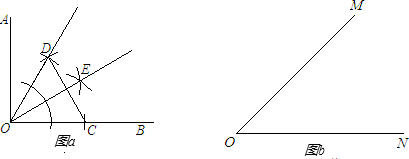
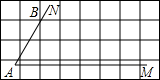 (2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
(2012•天津)“三等分任意角”是数学史上一个著名问题.已知一个角∠MAN,设∠α=
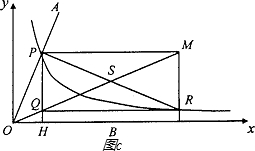
 的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB=
的图象交于点P,以P为圆心、2OP长为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线,两直线相交于点M,连接OM得到∠MOB,则∠MOB= ∠AOB.要明白帕普斯的方法,请研究以下问题:
∠AOB.要明白帕普斯的方法,请研究以下问题: )、R(b,
)、R(b, ),求直线OM对应的函数关系式(用含a、b的代数式表示).
),求直线OM对应的函数关系式(用含a、b的代数式表示). ∠AOB.
∠AOB.