
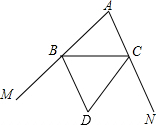
 已知:如图,BD,CD分别是△ABC的外角∠MBC、∠NCB的平分线,且交于点D.求证:点D在∠A的平分线上.
已知:如图,BD,CD分别是△ABC的外角∠MBC、∠NCB的平分线,且交于点D.求证:点D在∠A的平分线上. 分析 先过D作DE⊥BC于E,DF⊥AB,交AB延长线于F,作DG⊥AC,交AC延长线于G,由于BD是∠CBF的角平分线,DE⊥BC,DF⊥AB,利用角平分线的性质可得DE=DF,同理DE=DG,等量代换可得DF=DG,而DF⊥AB,DG⊥AC,再根据角平分线的判定定理可知点D在∠BAC的角平分线上.
解答 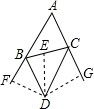 解:过D作DE⊥BC于E,DF⊥AB,交AB延长线于F,作DG⊥AC,交AC延长线于G,
解:过D作DE⊥BC于E,DF⊥AB,交AB延长线于F,作DG⊥AC,交AC延长线于G,
∵BD是∠CBF的角平分线,DE⊥BC,DF⊥AB,
∴DE=DF,
同理可得DE=DG,
∴DF=DG,
又∵DF⊥AB,DG⊥AC,
∴点D在∠BAC的角平分线上.
点评 本题考查了角平分线的性质以及判定定理,解题的关键是作辅助线,并证明DF=DG.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
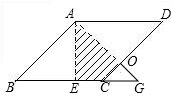 如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?
如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折后得△AGE,那么△AGE与四边形AECD重叠部分的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
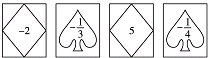
 的卡片,那么加上卡片上的数字,如果抽到形如
的卡片,那么加上卡片上的数字,如果抽到形如 的卡片,那么减去卡片上的数字;
的卡片,那么减去卡片上的数字;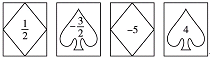
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
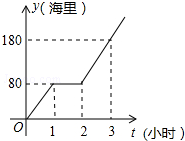 diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.
diaoyudao自古就是中国领土,中国政府已对钓鱼开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com