

分析 因为∠ABC和∠APC都是弧AC对着的圆周角,所以∠ABC=∠APC,即同弧所对的圆周角相等,同理可得∠ACB=∠APB,进而可知道小明使用的是圆周角的哪个性质;
深入探究:△ABC仍是等腰三角形,由圆的内接四边形定理以及圆周角定理证明再结合已知条件证明∠ABC=∠ACB即可得到AB=AC;
拓展提高:作直径CH,连结AH,由圆周角定理以及其同理和切线的性质定理再结合已知条件证明∠ABC=∠ACB,即可得到AB=AC.
解答 解:问题情境:同弧所对的圆周角相等,
深入探究:△ABC仍是等腰三角形,理由如下:
∵∠ABC+∠APC=180°,∠APN+∠APC=180°,
∴∠ABC=∠APN.
∵PA 平分∠MPN,
∴∠APB=∠APN,
∴∠ABC=∠APB.
而∠APB=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
拓展提高:△ABC仍是等腰三角形理由如下:
作直径CH,连结AH,
∵CH为直径,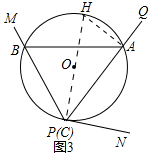
∴∠AHC=90°,
∴∠H+∠ACH=90°.
∵CN与圆O相切,
∴CN⊥CH,
∴∠ACN+∠ACH=90°,
∴∠ACN=∠H.
∵∠ABC=∠H,
∴∠ACN=∠ABC.
∵PA 平分∠MPN,
∴∠ACB=∠CAN.
∴∠ABC=∠ACB,
∴AB=AC.
点评 本题考查了和圆有关的综合性题目,用到的知识点有圆周角定义及其推论、角平分线的定义、圆的内接四边形定理以及切线的性质定理,题目的设计新颖,对学生理解问题的能力要求较高,特别是拓展提高部分正确作出图形的辅助线是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
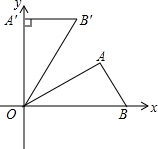 如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.
如图,在平面直角坐标系中,Rt△OAB的斜边OB在x轴的正半轴上,点A在第一象限,将△OAB,使点O按逆时针方向旋转至△OA′B′,使点A的对应点A′落在y轴的正半轴上,已知OB=2,∠AOB=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知第一象限内的点A在反比例函数y=$\frac{\sqrt{6}}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{\sqrt{6}}{3}$.
如图,已知第一象限内的点A在反比例函数y=$\frac{\sqrt{6}}{x}$上,第二象限的点B在反比例函数y=$\frac{k}{x}$上,且OA⊥OB,∠A=30°,则k的值为-$\frac{\sqrt{6}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 80% | B. | 60% | C. | 40% | D. | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$b2 | B. | -$\frac{1}{8}$b2 | C. | $\frac{1}{16}$b2 | D. | -$\frac{1}{16}$b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com