
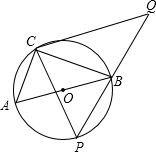
 如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为 ,tan∠ABC=
,tan∠ABC= ,则CQ的最大值是
,则CQ的最大值是


 =
= ,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=
,然后根据圆周角定理得到∠A=∠P,则可证得△ACB∽△PCQ,利用相似比得CQ=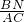 •PC=
•PC= PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可.
PC,PC为直径时,PC最长,此时CQ最长,然后把PC=5代入计算即可. ,
, =
= ,
,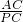 =
= ,
, •PC=
•PC= PC,
PC, ×5=
×5= .
.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
| 1 | 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
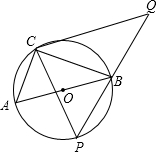 (2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为
(2013•德阳)如图,在⊙O上有定点C和动点P,位于直径AB的异侧,过点C作CP的垂线,与PB的延长线交于点Q,已知:⊙O半径为| 5 |
| 2 |
| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(湖南湘潭卷)数学(解析版) 题型:解答题
如图,在⊙O上位于直径AB的异侧有定点C和动点P,AC=AB,点P在半圆弧AB上运动(不与A、B两点重合),过点C作直线PB的垂线CD交PB于D点.
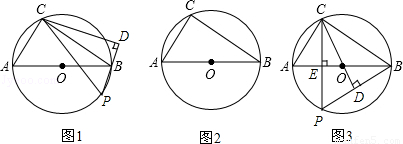
(1)如图1,求证:△PCD∽△ABC;
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;
(3)如图3,当点P运动到CP⊥AB时,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源:2013年四川省德阳市中考数学试卷(解析版) 题型:选择题
 ,tan∠ABC=
,tan∠ABC= ,则CQ的最大值是( )
,则CQ的最大值是( )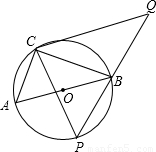
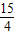
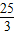
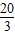
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com