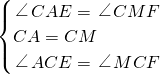证明:(1)∵△ACM,△CBN是等边三角形,
∴AC=MC,BC=NC,∠ACM=60°,∠NCB=60°,
∴∠ACM+∠MCN=∠NCB+∠MCN,
即:∠ACN=∠MCB,
在△CAN和△MCB中,
AC=MC,∠ACN=∠MCB,NC=BC,
∴△CAN≌△MCB(SAS),
∴∠CMB=∠CAN
又∵∠ACM=∠MCN=60°,AC=NC
∴△ACE≌△MCF
∴CE=CF.
(2)∵△CAN≌△CMB,
∴∠CAN=∠CMB,
又∵∠MCF=180°-∠ACM-∠NCB=180°-60°-60°=60°,
∴∠MCF=∠ACE,
在△CAE和△CMF中,
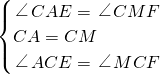
∴△CAE≌△CMF(ASA),
∴CE=CF,
∴△CEF为等腰三角形,
又∵∠ECF=60°,
∴△CEF为等边三角形.
∴∠CEF=∠MCA=60°
∴EF∥AB
分析:(1)由等边三角形可得其对应线段相等,对应角相等,进而可由SAS得到△CAN≌△MCB,结论得证;
(2)由(1)中的全等可得∠CAN=∠MCB,进而得出∠MCF=∠ACE,由ASA得出△CAE≌△CMF,即CE=CF,又ECF=60°,所以△CEF为等边三角形.从而利用等边三角形的性质判定平行.
点评:本题主要考查了全等三角形的判定及性质以及等边三角形的判定问题,能够掌握并熟练运用.

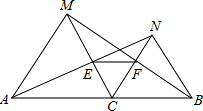 已知如图,点C为线段AB上一点,△ACM、△CBN都是等边三角形,AN交CM于点E,BM交CN于点F,求证:
已知如图,点C为线段AB上一点,△ACM、△CBN都是等边三角形,AN交CM于点E,BM交CN于点F,求证: