

分析 (1)利用待定系数法求出抛物线的解析式,令y=0解方程,求出点C的坐标;
(2)如答图1所示,由△CEF∽△COA,根据比例式列方程求出OE的长度;
(3)如答图2所示,若△DMN是等腰三角形,可能有三种情形,需要分类讨论;
(4)当正方形DEFG与△ABC的重叠部分为五边形时,如答图3所示.利用S=S正方形DEFG-S梯形MEDN-S△FJK求出S关于t的表达式.
解答 解:(1)∵抛物线y=-$\frac{1}{8}$x2+mx+n经过点A(0,3),B(2,3),
∴$\left\{\begin{array}{l}{n=3}\\{-\frac{1}{8}×{2}^{2}+2m+n=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=\frac{1}{4}}\\{n=3}\end{array}\right.$,
∴抛物线的解析式为:y=-$\frac{1}{8}$x2+$\frac{1}{4}$x+3.
令y=0,即-$\frac{1}{8}$x2+$\frac{1}{4}$x+3=0,
解得x=6或x=-4,
∵点C位于x轴正半轴上,
∴C(6,0).
(2)当正方形的顶点F恰好落在线段AC上时,如答图1所示: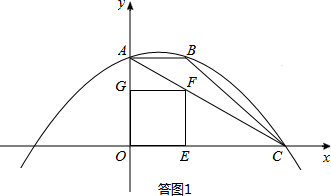
设OE=x,则EF=x,CE=OC-OE=6-x.
∵EF∥OA,
∴△CEF∽△COA,
∴$\frac{EF}{OA}$=$\frac{CE}{CO}$,即$\frac{x}{3}$=$\frac{6-x}{6}$,
解得x=2.
∴OE=2.
(3)存在满足条件的t.理由如下:
如答图2所示,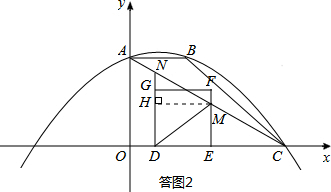
易证△CEM∽△COA,∴$\frac{EM}{OA}$=$\frac{CE}{CO}$,即$\frac{EM}{3}$=$\frac{4-t}{6}$,得ME=2-$\frac{1}{2}$t.
过点M作MH⊥DN于点H,则DH=ME=2-$\frac{1}{2}$t,MH=DE=2.
易证△MHN∽△COA,∴$\frac{NH}{OA}$=$\frac{MH}{OC}$,即$\frac{NH}{3}$=$\frac{2}{6}$,得NH=1.
∴DN=DH+HN=3-$\frac{1}{2}$t.
在Rt△MNH中,MH=2,NH=1,由勾股定理得:MN=$\sqrt{5}$.
当△DMN是等腰三角形时,分三种情况:
①若DN=MN,则3-$\frac{1}{2}$t=$\sqrt{5}$,解得t=6-2$\sqrt{5}$;
②若DM=MN,则DM2=MN2,即22+(2-$\frac{1}{2}$t)2=($\sqrt{5}$)2,
解得t=2或t=6(不合题意,舍去);
③若DM=DN,则DM2=DN2,即22+(2-$\frac{1}{2}$t)2=(3-$\frac{1}{2}$t)2,解得t=1.
综上所述,当t=1或2或6-2$\sqrt{5}$时,△DMN是等腰三角形.
(4)当正方形DEFG与△ABC的重叠部分为五边形时,如答图3所示: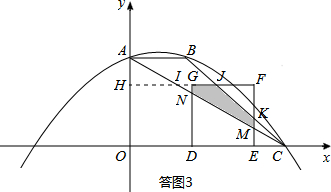
设EF、DG分别与AC交于点M、N,由(3)可知:ME=2-$\frac{1}{2}$t,DN=3-$\frac{1}{2}$t.
设直线BC的解析式为y=kx+b,将点B(2,3)、C(6,0)代入得:
$\left\{\begin{array}{l}{2k+b=3}\\{6k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=\frac{9}{2}}\end{array}\right.$,
∴y=-$\frac{3}{4}$x+$\frac{9}{2}$.
设直线BC与EF交于点K,
∵xK=t+2,∴yK=-$\frac{3}{4}$xK+$\frac{9}{2}$=-$\frac{3}{4}$t+3,
∴FK=yF-yK=2-(-$\frac{3}{4}$t+3)=$\frac{3}{4}$t-1;
设直线BC与GF交于点J,
∵yJ=2,
∴2=-$\frac{3}{4}$xJ+$\frac{9}{2}$,得xJ=$\frac{10}{3}$,
∴FJ=xF-xJ=t+2-$\frac{10}{3}$=t-$\frac{4}{3}$.
∴S=S正方形DEFG-S梯形MEDN-S△FJK
=DE2-$\frac{1}{2}$(ME+DN)•DE-$\frac{1}{2}$FK•FJ
=22-$\frac{1}{2}$[(2-$\frac{1}{2}$t)+(3-$\frac{1}{2}$t)]×2-$\frac{1}{2}$($\frac{3}{4}$t-1)(t-$\frac{4}{3}$)
=-$\frac{3}{8}$t2+2t-$\frac{5}{3}$.
过点G作GH⊥y轴于点H,交AC于点I,则HI=2,HJ=$\frac{10}{3}$,
∴t的取值范围是:2<t<$\frac{10}{3}$.
∴S与t的函数关系式为:S=-$\frac{3}{8}$t2+2t-$\frac{5}{3}$(2<t<$\frac{10}{3}$).
点评 本题是二次函数综合题,考查了待定系数法求二次函数、一次函数的解析式,相似三角形的判定与性质,勾股定理,等腰三角形的性质,图形面积的计算等知识,考查了运动型问题、存在型问题和分类讨论的数学思想,难度较大.解题关键是理解图形的运动过程.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
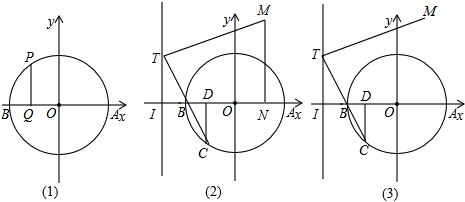
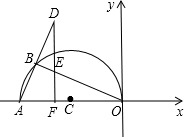 在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.
在平面直角坐标系中,点A(-5,0),以OA为直径在第二象限内作半圆C,点B是该半圆周上一动点,连接OB、AB,作点A关于点B的对称点D,过点D作x轴垂线,分别交直线OB、x轴于点E、F,点F为垂足,当DF=4时,线段EF=$\frac{3}{2}$或6.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:
甲、乙两车分别从M,N两地沿同一公路相向匀速行驶,两车分别抵达N,M两地后即停止行驶.已知乙车比甲车提前出发,设甲、乙两车之间的路程S(km),乙行驶的时间为t(h),S与t的函数关系如图所示.有下列说法:| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com