
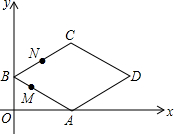
 ��ƽ��ֱ������ϵ�У��ı���ABCD�����Σ����е�B�������ǣ�0��2������D�������ǣ�$4\sqrt{3}$��2������M�͵�N���������㣬���е�M�ӵ�B������BA��ÿ��1����λ���ٶ��������˶�������A��ֹͣ��ͬʱ��N��B�����������BC��CD��ÿ��2����λ���ٶ��������˶����������һ��ֹͣ�˶�������һ��Ҳֹͣ�˶�����M��N������˶�ʱ��Ϊx����BMN�������y������ͼ�����ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������
��ƽ��ֱ������ϵ�У��ı���ABCD�����Σ����е�B�������ǣ�0��2������D�������ǣ�$4\sqrt{3}$��2������M�͵�N���������㣬���е�M�ӵ�B������BA��ÿ��1����λ���ٶ��������˶�������A��ֹͣ��ͬʱ��N��B�����������BC��CD��ÿ��2����λ���ٶ��������˶����������һ��ֹͣ�˶�������һ��Ҳֹͣ�˶�����M��N������˶�ʱ��Ϊx����BMN�������y������ͼ�����ܱ�ʾy��x�ĺ�����ϵ��ͼ������ǣ�������| A�� | 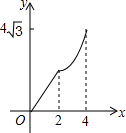 | B�� | 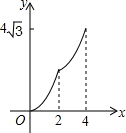 | C�� | 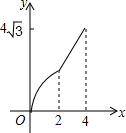 | D�� | 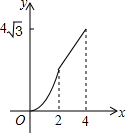 |
���� �������⣬������������˶��仯��д����N��BC���˶�ʱ��BMN���������д������N��CD���˶�ʱ��BMN����������ɵó�����Ĵ𰸣�
��� �⣺��0��x��2ʱ��
��ͼ1��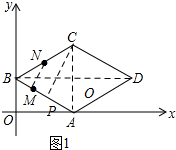
����BD��AC�����ڵ�O������NM������C��CP��AB����Ϊ��P��
���CPB=90�㣬
���ı���ABCD�����Σ����е�B�������ǣ�0��2������D�������ǣ�$4\sqrt{3}$��2����
��BO=2$\sqrt{3}$��CO=2��
��BC=AB=$\sqrt{B{O}^{2}+C{O}^{2}}$=4��
��AC=4��
���ABC�ǵȱ������Σ�
���ABC=60�㣬
��CP=BC•sin60��=4��$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$��
BP=2��
BN=2x��BM=x��
$\frac{BM}{BP}=\frac{x}{2}$��$\frac{BN}{BC}=\frac{x}{2}$��
��$\frac{BM}{BP}=\frac{BN}{BC}$��
�֡ߡ�NBM=��CBP��
���NBM�ס�CBP��
���NMB=��CPB=90�㣬
��y=$\frac{1}{2}$•x•$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2��
��2��x��4ʱ����ͼ2��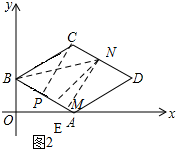
��NE��AB������ΪE��
���ı���ABCD�����Σ�
��AB��CD��
��NE=CP=2$\sqrt{3}$��
BM=x��
��y=$\frac{1}{2}•x•2\sqrt{3}$=$\sqrt{3}x$��
��y=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}{x}^{2}}&{��0��x��2��}\\{\sqrt{3}x}&{��2��x��4��}\end{array}\right.$��
��ѡD��
���� ������Ҫ�����˶�������ĺ���ͼ�����⣬���ݼ���֪ʶ�����������ʽ�ǽ���Ĺؼ���Ҫע�������ܽᣮ


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��1 | C�� | -1��x��2 | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
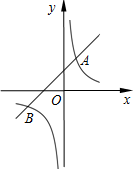 ��ͼ����֪һ�κ���y1=k1x+4�뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ���ڵ�A��2��m����B��-6��-2����
��ͼ����֪һ�κ���y1=k1x+4�뷴��������y2=$\frac{{k}_{2}}{x}$��ͼ���ڵ�A��2��m����B��-6��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3cm | B�� | 8cm | C�� | 3cm��8cm | D�� | ���ϴ𰸾����� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com