
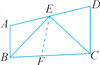
【题目】如图,在四边形ABCD中,AB∥DC,BE,CE分别平分∠ABC,∠BCD,且点E在AD上.求证:BC=AB+CD.
科目:初中数学 来源: 题型:
【题目】阅读理解题:
如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
![]()
(1)可求得x= .
(2)第2017个格子中的数为 ;
(3)前n个格子中所填整数之和是否可能为2020?若能,求出n的值,若不能,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
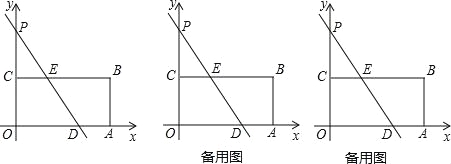
【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0)、(12,6),直线y=﹣![]() x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
x+b与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣![]() x+b平分矩形OABC的面积,求b的值;
x+b平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,当直线y=﹣![]() x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
x+b绕点P顺时针旋转时,与直线BC和x轴分别交于点N、M,问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长;若不存在,请说明理由;
(3)在(1)的条件下,将矩形OABC沿DE折叠,若点O落在边BC上,求出该点坐标;若不在边BC上,求将(1)中的直线沿y轴怎样平移,使矩形OABC沿平移后的直线折叠,点O恰好落在边BC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宏远商贸公司有A、B两种型号的商品需运出,这两种商品的体积和质量分别如下表所示:
体积(m3/件) | 质量(吨/件) | |
A型商品 | 0.8 | 0.5 |
B型商品 | 2 | 1 |
(1)已知一批商品有A、B两种型号,体积一共是20m3,质量一共是10.5吨,求A、B两种型号商品各有几件?
(2)物流公司现有可供使用的货车每辆额定载重3.5吨,容积为6m3,其收费方式有以下两种:
①按车收费:每辆车运输货物到目的地收费600元;
②按吨收费:每吨货物运输到目的地收费200元.
要将(1)中的商品一次或分批运输到目的地,宏远商贸公司应如何选择运送、付费方式运费最少并求出该方式下的运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)一条直线可以把平面分成两个部分(或区域),如图,两条直线可以把平面分成几个部分?三条直线可以把平面分成几个部分?试画图说明.

(2)四条直线最多可以把平面分成几个部分?试画出示意图,并说明这四条直线的位置关系.
(3)平面上有![]() 条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的
条直线,每两条直线都恰好相交,且没有三条直线交于一点,处于这种位置的![]() 条直线分一个平面所成的区域最多,记为
条直线分一个平面所成的区域最多,记为![]() ,试研究
,试研究![]() 与
与![]() 之间的关系.
之间的关系.
思维方法天地
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com