
【题目】从![]() 开始,连续的奇数相加,它们和的情况如表所示:
开始,连续的奇数相加,它们和的情况如表所示:
加数的个数 | 连续奇数的和 |
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )当
)当![]() 的值为__________.
的值为__________.
(![]() )用含
)用含![]() 的代数式表示
的代数式表示![]() 个连续奇数之和
个连续奇数之和![]() 的公式,
的公式, ![]() __________.
__________.
用含![]() 的代数式表示从
的代数式表示从![]() 开始的第
开始的第![]() 个连续奇数是__________.
个连续奇数是__________.
(![]() )根据规律计算
)根据规律计算![]() .
.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() ;(
;(![]() )
)![]() .
.
【解析】试题分析:(1)仔细观察给出的等式可发现从1开始连续两个奇数和是22,连续3个奇数和是32,连续4个,5个奇数和分别为42,52从而推出从1开始几个连续奇数和等于几的平方,根据此规律解题即可.
(2)根据奇数的表示方法可得从1开始的第 n个连续奇数,再根据(1)中规律可得n个连续奇数之和S的公式;
(3)利用(2)中规律可得结论.
试题解析:解:(1)∵从1开始的连续2个奇数和是22,连续3个奇数和是32,连续4个,5个奇数和分别为42,52,…
由此猜想,从1开始的连续11个奇数和是112=121,故答案为:121;
(2)由(1)知,从1开始的第 n个连续奇数是2n﹣1,从1开始的连续n个奇数的和S=n2,故答案为:n2,2n﹣1.
(3)1001+1003+1005+…+2013+2015+2017=10092﹣5002=768081.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE. 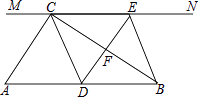
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
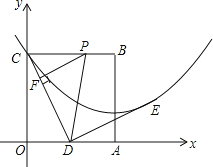
(1)求抛物线的解析式;
(2)点P从点C出发,沿射线CB每秒1个单位长度的速度运动,运动时间为t秒.过点P作PF⊥CD于点F,当t为何值时,以点P,F,D为顶点的三角形与△COD相似?
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
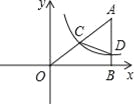
【题目】如图,在平面直角坐标系中A点的坐标为(8,y),AB⊥x轴于点B,sin∠OAB=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)若函数y=3x与y=![]() 的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
的图象的另一支交于点M,求三角形OMB与四边形OCDB的面积的比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区为了解小区500户居民家庭平均月使用塑料袋的数量情况,随机调查了10户居民家庭月使用塑料袋的数量,结果如下(单位:只):65,70,85,74,86,78,74,92,82,94.
根据统计情况,估计该小区这500户家庭每月一共使用塑料袋_________只.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】16,如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2017个点的坐标为
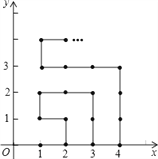
查看答案和解析>>
科目:初中数学 来源: 题型:
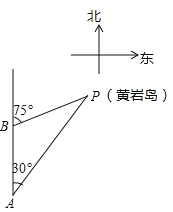
【题目】如图,三沙市一艘海监船某天在黄岩鸟P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据: ![]() ≈1.414,结果精确到0.1)
≈1.414,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P为∠EAF平分线上一点,PB⊥AE于B,PC⊥AF于C,点M,N分别是射线AE,AF上的点,且PM=PN. 
(1)如图1,当点M在线段AB上,点N在线段AC的延长线上时,求证:BM=CN;
(2)在(1)的条件下,直接写出线段AM,AN与AC之间的数量关系;
(3)如图2,当点M在线段AB的延长线上,点N在线段AC上时,若AC:PC=2:1,且PC=4,求四边形ANPM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com