解:(1)在梯形ABCD中,AD∥BC,AB=DC,∠ABC=70°,
∴∠A=∠D=110°,
∴∠AEB+∠ABE=180°-110°=70°.
∵∠BEF=110°,
∴∠AEB+∠DEF=180°-110°=70°,
∴∠ABE=∠DEF.
∴△ABE∽△DEF,
∴

,
又∵E为AD中点,AB=DC=AD=9,
∴AE=DE=4.5,AB=9,
∴DF=

=

=2.25;
(2)不存在.
假设点E存在,设AE=x,则DE=9-x,
又F为CD中点,得到DF=

CD=4.5,
由(1)得

,
可得

,
整理得x
2-9x+40.5=0,
∵△=81-4×40.5=-81<0,即方程无实数根,
∴E点不存在.
分析:(1)由AD与BC平行得到同旁内角互补,又AB=DC,得到同一底上的两个角相等,从而得到∠A=∠D=110°,在三角形ABE中,利用三角形的内角和定理得到其他两角之和为70°,又∠BEF=110°,根据平角定义得到剩下的两个角之和也为70°,等量代换可得∠ABE=∠DEF,根据两对对应角相等的两三角形相似可得三角形ABE与三角形DEF相似,由相似得比例,由E为AD中点,求出AE与ED的长,把各边的长代入比例式,即可求出DF的长;
(2)假设存在这样的E使F为CD的中点,则DF等于CD的一半,即为4.5,设AE=x,则DE=9-x,把表示出的各边的长代入(1)得到的比例式中,得到关于x的一元二次方程,由根的判别式小于0得到此方程无解,故假设错误,所以不存在这样的E使F为DC中点.
点评:此题考查了相似三角形的判断与性质,等腰梯形的性质以及一元二次方程的解法,是一道探究型的题,第一小问注意利用角度之间的转换,证两三角形相似是解题的关键;第二小问,先对结论作出存在的假设,然后由假设出发,结合已知的条件或已挖掘的结论,结合图形,借助数学思想和方法,进行正确的计算和推理,得出结果,检验其结果是否与题设、定理及公理相符,若无矛盾,说明假设正确;若矛盾,假设错误,故不存在.

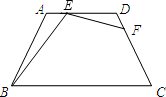 (点E与点A,D不重合),且∠BEF=110°.
(点E与点A,D不重合),且∠BEF=110°. ,
, =
= =2.25;
=2.25; CD=4.5,
CD=4.5, ,
, ,
,

 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )