Question

【题目】如图1在平面直角坐标系中，⊙O1与x轴切于A（﹣3，0）与y轴交于B、C两点，BC=8，连AB．

（1）求证：∠ABO1=∠ABO；

（2）求AB的长；

（3）如图2，过A、B两点作⊙O2与y轴的正半轴交于M，与O1B的延长线交于N，当⊙O2的大小变化时， BM﹣BN的值是否发生不变？并说明理由？

Answer 1

【答案】（1）证明见解析；

（2）AB=；

（3）BM﹣BN的值不变，理由见解析.

【解析】试题分析：（1）连接O1A，由圆O1与x轴切于A，根据切线的性质得到O1A垂直于OA，由OB与AO垂直，根据平面内垂直于同一条直线的两直线平行，得到O1A与OB平行，根据两直线平行内错角相等，得到一对内错角相等，再由O1A=O1B，根据等边对等角可得出一对角相等，等量代换可得出∠ABO1=∠ABO，得证；

（2）作O1E⊥BC于点E，根据垂径定理得到E为BC的中点，由点O1的坐标为（，-2），可求得OE=O1B=O1A=2，O1E=OA=，然后由勾股定理求得BE的长，继而求得OB与OC以及AB的长，；

（3）两个结论中，①BM-BN的值不变正确，理由为：在MB上取一点G，使MG=BN，连接AM、AN、AG、MN，由∠ABO1为四边形ABMN的外角，根据圆内接四边形的外角等于它的内对角，可得出∠ABO1=∠NMA，再由∠ABO1=∠ABO，等量代换可得出∠ABO=∠NMA，然后利用同弧所对的圆周角相等可得出∠ABO=∠ANM，等量代换可得出∠NMA=∠ANM，根据等角对等边可得出AM=AN，再由同弧所对的圆周角相等，及OM=BN，利用SAS可得出三角形AMG与三角形ABN全等，根据全等三角形的对应边相等可得出AG=AB，由AO与BG垂直，根据三线合一得到O为BG的中点，根据OB的长求出BG的长，然后BM-BN=BM-MG=BG，由BG为常数得到BM-BN的长不变，得证．

试题解析：（1）连接O1A，则O1A⊥OA，

又∵OB⊥OA，

∴O1A∥OB，

∴∠O1AB=∠ABO，

又∵O1A=O1B，

∴∠O1AB=∠O1BA，

∴∠ABO1=∠ABO；

（2）过点作O1E⊥BC于点E，

∴BE=CE，

∵点O1的坐标为（，-2），

∴OE=O1B=O1A=2，O1E=OA=，

∴在Rt△BO1E中，BE=，

∴OB=OE-BE=2-1=1，OC=OE+CE=2+1=3，

∴；

（3）①正确．理由为：在MB上取一点G，使MG=BN，连接AM、AN、AG、MN，

∵∠ABO1为四边形ABMN的外角，

∴∠ABO1=∠NMA，

又∵∠ABO1=∠ABO，

∴∠ABO=∠NMA，

又∵∠ABO=∠ANM，

∴∠AMN=∠ANM，

∴AM=AN，

∵∠AMG和∠ANB都为所对的圆周角，

∴∠AMG=∠ANB，

∵在△AMG和△ANB中，

，

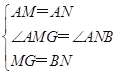∴△AMG≌△ANB（SAS），

∴AG=AB，

∵AO⊥BG，

∴BG=2BO=2，

∴BM-BN=BM-MG=BG=2其值不变．

考点: 圆的综合题.