
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
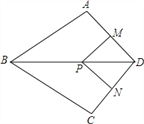
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
【答案】(1)(2)证明见解析
【解析】试题分析:(1)根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD,由全等三角形的性质即可得到:∠ADB=∠CDB;
(2)若∠ADC=90°,由(1)中的条件可得四边形MPND是矩形,再根据两边相等的四边形是正方形即可证明四边形MPND是正方形.
证明:(1)∵对角线BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
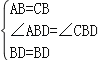 ,
,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形MPND是矩形,
∵∠ADB=∠CDB,
∴∠ADB=45°
∴PM=MD,
∴四边形MPND是正方形.


科目:初中数学 来源: 题型:
【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
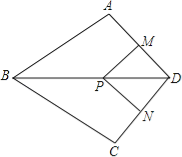
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的进度均保持不变).储运部库存物资w(吨)与时间t(小时)之间的函数关系如图所示,请问这批物资从开始调进到全部调出需要多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
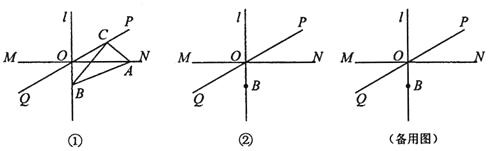
【题目】如图![]() ,直线
,直线![]() ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且![]() 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,![]() 点C在直线PQ上运动
点C在直线PQ上运动![]() 连接BC过点C作
连接BC过点C作![]() ,交直线MN于点A,连接
,交直线MN于点A,连接![]() 点A、C与点O都不重合
点A、C与点O都不重合![]() .
.
![]() 小明经过画图、度量发现:在
小明经过画图、度量发现:在![]() 中,始终有一个角与
中,始终有一个角与![]() 相等,这个角是________________;
相等,这个角是________________;
![]() 当
当![]() 时,在图
时,在图![]() 中画出示意图并证明
中画出示意图并证明![]() ;
;
![]() 探索
探索![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( ) 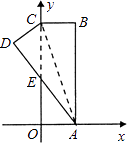
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
项目品牌 | 单价/元 | 购买数量/台 | 购买费用/元 |
A | 800 | x |
|
B | 1000 |
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车和一辆小轿车同时从甲地出发,货车匀速行驶至乙地,小轿车中途停车休整2h后提速行驶至乙地.设行驶时间为x( h),货车的路程为y1( km),小轿车的路程为y2( km ),图中的线段OA与折线OBCD分别表示y1,y2与x之间的函数关系.
(1)甲乙两地相距_____km,m=_____;
(2)求线段CD所在直线的函数表达式;
(3)小轿车停车休整后还要提速行驶多少小时,与货车之间相距20km?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com