
分析 根据相反数、倒数、绝对值求出m+n=0,$\frac{m}{n}$=-1,ab=1,x=6或-2,代入求出即可.
解答 解:∵m,n互为相反数,且mn≠0,a,b互为倒数,|x-2|=4,
∴m+n=0,$\frac{m}{n}$=-1,ab=1,x-2=±4,
∴x=6或-2,
当x=6时,x3-(1+m+n+ab)x2+($\frac{m}{n}$)2017=63-(1+0+1)×62+(-1)2017=143;
当x=-2时,x3-(1+m+n+ab)x2+($\frac{m}{n}$)2017=(-2)3-(1+0+1)×(-2)2+(-1)2017=-17.
点评 本题考查了求代数式的值、倒数、绝对值、相反数等知识点,能求出求出m+n=0、$\frac{m}{n}$=-1、ab=1、x=6或-2是解此题的关键.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
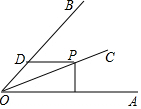 如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )
如图,OC平分∠AOB=60°,且∠AOB=60°,点P为OC上任意点,PM⊥OA于M,PD∥OA,交OB于D,若OM=6,则PD的长为( )| A. | 3 | B. | 4 | C. | 4.5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.
如图,已知△ABC中,点F在边AB上,且AF=$\frac{2}{5}$AB、过A作AG∥BC交CF的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com