
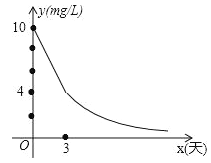
����Ŀ����2016����ʡ���Ƹ��У������ֶ�ij��ҵ����������м�⣬�����ʾ��������ˮ�������Ũ�ȳ��꣬�������Ũ�ȳ������������1.0mg/L��������Ҫ�����ҵ�������ģ���15�����ڣ���15�죩���۴�꣮���Ĺ����У�������ˮ�������Ũ��y��mg/L����ʱ��x���죩�ı仯������ͼ��ʾ�������߶�AB��ʾǰ3��ı仯���ɣ��ӵ�3����������ˮ�������Ũ��y��ʱ��x�ɷ�������ϵ��
��1�������Ĺ����������Ũ��y��ʱ��x�ĺ�������ʽ��
��2������ҵ������ˮ�������Ũ�ȣ��ܷ���15�����ڲ��������������1.0mg/L��Ϊʲô��
���𰸡���1��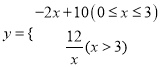 ����2���ܣ�
����2���ܣ�
�������������������1����������ۣ��ٵ�0��x��3ʱ�����߶�AB��Ӧ�ĺ�������ʽΪy=kx+b����A��0��0����B��3��4������ó������飬�ⷽ���鼴�ɣ��ڵ�x��3ʱ����y=![]() ���ѣ�3��4���������m��ֵ���ɣ�
���ѣ�3��4���������m��ֵ���ɣ�
��2����![]() =1���ó�x=12��15�����ɵó����ۣ�
=1���ó�x=12��15�����ɵó����ۣ�
�����������1����������ۣ�
�ٵ�0��x��3ʱ�����߶�AB��Ӧ�ĺ�������ʽΪy=kx+b��
��A��0��0����B��3��4�������![]() ����ã�
����ã� ![]() ����y=��2x+10��
����y=��2x+10��
�ڵ�x��3ʱ����![]() ���ѣ�3��4������ã�m=3��4=12����
���ѣ�3��4������ã�m=3��4=12����![]() ��
��
����������  ��
��
��2���ܣ��������£�
��![]() =1����x=12��15��������15�����ڲ��������������1.0mg/L��
=1����x=12��15��������15�����ڲ��������������1.0mg/L��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() �������ύ��A��B��C���㣬����C��0��3������BAC��ƽ����AE��y���ڵ�D����BC�ڵ�E������D��ֱ��l������AC��AB�ֱ��ڵ�M��N��
�������ύ��A��B��C���㣬����C��0��3������BAC��ƽ����AE��y���ڵ�D����BC�ڵ�E������D��ֱ��l������AC��AB�ֱ��ڵ�M��N��
��1��ֱ��д��a��ֵ����A�����꼰�����ߵĶԳ��
��2����PΪ�����ߵĶԳ�����һ���㣬����PADΪ���������Σ������P�����ꣻ
��3��֤������ֱ��l�Ƶ�D��תʱ��![]() ��Ϊ��ֵ��������ö�ֵ��
��Ϊ��ֵ��������ö�ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��1=��2��AC=AD��Ҫʹ��ABC�ա�AED����������һ����������ô�ڢ�AB=AE����BC=ED���ۡ�C=��D���ܡ�B=��E�����ĸ���ϵ�п���ѡ�����(����)
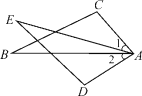
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̾�����ѧ����Ʒ������ÿ��280Ԫ�ļ۸�ij���ͺŵ�ѧϰ������ÿ��360Ԫ���ۼ�����ʱ��ÿ�¿��۳�60����Ϊ���������ۣ��þ����̲�ȡ���۵ķ�ʽ�������������з��֣����ÿ��ѧϰ������1Ԫ����ôÿ�¾Ϳ��Զ��۳�5����
![]() ����ǰ��������ѧϰ��ÿ�µ������Ƕ���Ԫ��
����ǰ��������ѧϰ��ÿ�µ������Ƕ���Ԫ��
![]() ��������������ѧϰ��ÿ�µ�����Ҫ�ﵽ7200Ԫ���Ҿ����������ڹ˿ͣ���ÿ��ѧϰ��Ӧ���۶���Ԫ��
��������������ѧϰ��ÿ�µ�����Ҫ�ﵽ7200Ԫ���Ҿ����������ڹ˿ͣ���ÿ��ѧϰ��Ӧ���۶���Ԫ��
![]() ��
��![]() �������У������ɺã��������ֿ�ʼ�Ǽۣ��Ǽۺ�ÿ����������ѧϰ���������ܴﵽ10580Ԫ�����ܣ�������Ƕ���Ԫ�������ܣ���˵�����ɣ�
�������У������ɺã��������ֿ�ʼ�Ǽۣ��Ǽۺ�ÿ����������ѧϰ���������ܴﵽ10580Ԫ�����ܣ�������Ƕ���Ԫ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ���ǵ���������
���ǵ���������![]() һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
һ����������һ��������Ա��ཻ�������뽻��֮����߶ΰ���������ηָ������С�����Σ�����ֵõ�����С��������һ��Ϊ���������Σ���һ����ԭ���������ƣ����ǰ������߶ν�����������ε������ָ��ߣ�
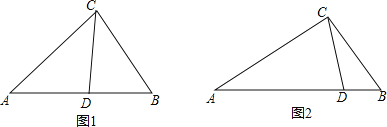
![]() ��ͼ1����
��ͼ1����![]() �У�CDΪ��ƽ���ߣ�
�У�CDΪ��ƽ���ߣ�![]() ��
��![]() ����֤��CDΪ
����֤��CDΪ![]() �������ָ��ߣ�
�������ָ��ߣ�
![]() ��
��![]() ��
��![]() ��CD��
��CD��![]() �������ָ��ߣ���
�������ָ��ߣ���![]() Ϊ���������Σ���
Ϊ���������Σ���![]() �Ķ�����
�Ķ�����
![]() ��ͼ2��
��ͼ2��![]() �У�
��![]() ��
��![]() ��CD��
��CD��![]() �������ָ��ߣ���
�������ָ��ߣ���![]() ����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
����CDΪ�ױߵĵ��������Σ��������ָ���CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC��AD����ABC�Ľ�ƽ���ߣ���OΪAB���е㣬����DO���ӳ�����E��ʹOE=OD������AE��BE��

��1����֤���ı���AEBD�Ǿ��Σ�
��2������ABC����ʲô����ʱ������AEBD�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ֱ��AB��CD�ڵ�O��OEƽ�֡�BOD��OFƽ�֡�COB����AOD����BOE��5��2�����AOF���ڣ�������

A. 140�� B. 130�� C. 120�� D. 110��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���BAC=90�㣬AB=AC��D��AC����һ���㣬CE��BD��E��

��1����ͼ��1������BDƽ����ABCʱ��������ECD�Ķ��������ӳ�CE��BA���ӳ����ڵ�F����ȫͼ�Σ�̽��BD��EC��������ϵ����֤����Ľ��ۣ�
��2����ͼ��2��������A��AF��BE�ڵ�F�������߶�BE��CE��AF֮���������ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y��ax![]() +bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x
+bx+c��ͼ��������ƽ��3����λ��������ƽ��2����λ�����õ�ͼ��Ľ���ʽ��y��x![]() ��3x+5����a+b+c=__________��
��3x+5����a+b+c=__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com