
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
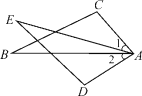
A. ①②③ B. ①②④ C. ①③④ D. ②③④
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
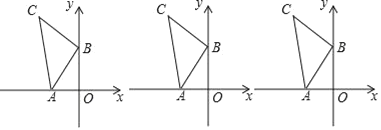
【题目】如图,在正方形网格中,每一个小正方形的边长为1.△ABC的三个顶点都在格点上,A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC向右平移6个单位的△A1B1C1,并写出C1的坐标 ;
(3)请画出△ABC关于原点O对称的△A2B2C2 , 并写出点C2的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
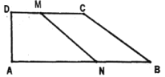
【题目】如图,在直角梯形ABCD中,DC∥AB,∠A=90°,AB=26cm,DC=18cm ,AD=4cm,动点M以1cm/s的速度从点D向点C运动,动点N从点B以2cm/s的速度向点A运动点M、N同时出发,当其中一个动点到达端点时停止运动,另一个动点也随之停止运动,设动点运动时间为t(s),四边形ANMD的面积y(![]() ),y关于x的函数解析式并写出定义域_____.
),y关于x的函数解析式并写出定义域_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,再填空解题:
①方程x2﹣x﹣6=0的根是x1=3,x2=﹣2,则x1+x2=1,x1x2=﹣6;
②方程2x2﹣7x+3=0的根是x1=![]() ,x2=3,则x1+x2=
,x2=3,则x1+x2=![]() ,x1x2=
,x1x2=![]() .
.
根据以上①②你能否猜出:
如果关于x的一元二次方程ax2+bx+c=0(a≠0,且a、b、c为常数,b2﹣4ac≥0)有两根x1、x2,那么x1+x2、x1x2与系数a、b、c有什么关系?请写出你的猜想并说明理由.
利用公式法求出方程的根即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小文同学统计了某小区部分居民每周使用共享单车的时间,并绘制了统计图,如图所示.下面有四个推断:
①小文此次一共调查了![]() 位小区居民
位小区居民
②每周使用时间不足![]() 分钟的人数多于
分钟的人数多于![]() 分钟的人数
分钟的人数
③每周使用时间超过![]() 分钟的人数超过调查总人数的一半
分钟的人数超过调查总人数的一半
④每周使用时间在![]() 分钟的人数最多
分钟的人数最多
根据图中信息,上述说法中正确的是( )

A.①④B.①③C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC≌△EDC.
(1)若DE∥BC(如图1),判断△ABC的形状并说明理由.
(2)连结BE,交AC于F,点H是CE上的点,且CH=CF,连结DH交BE于K(如图2).求证:∠DKF=∠ACB

查看答案和解析>>
科目:初中数学 来源: 题型:
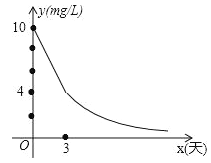
【题目】(2016江苏省连云港市)环保局对某企业排污情况进行检测,结果显示:所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改,在15天以内(含15天)排污达标.整改过程中,所排污水中硫化物的浓度y(mg/L)与时间x(天)的变化规律如图所示,其中线段AB表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度y与时间x成反比例关系.
(1)求整改过程中硫化物的浓度y与时间x的函数表达式;
(2)该企业所排污水中硫化物的浓度,能否在15天以内不超过最高允许的1.0mg/L?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(m,0),B(0,n),以B点为直角顶点在第二象限作等腰直角△ABC.
(1)求C点的坐标.
(2)在y轴右侧的平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com