
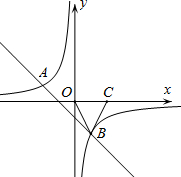
 (2012•河北区一模)如图,一次函数 y=kx+b 的图象与反比例函数 y=
(2012•河北区一模)如图,一次函数 y=kx+b 的图象与反比例函数 y=| m | x |
| m |
| x |
| 2 |
| x |
| 2 |
| x |
|
|
| 2 |
| x |
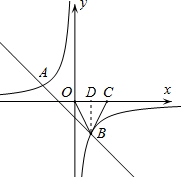
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 (2012•河北区一模)在今年我市体育学业水平考试女子800米耐力测试中,甲和乙测试所跑的路程S(米)与所用时间t(秒)之间的函数关系的图象分别为线段OA和折线OBCD.下列说法正确的是( )
(2012•河北区一模)在今年我市体育学业水平考试女子800米耐力测试中,甲和乙测试所跑的路程S(米)与所用时间t(秒)之间的函数关系的图象分别为线段OA和折线OBCD.下列说法正确的是( )查看答案和解析>>
科目:初中数学 来源: 题型:
出发地 目的地 运费(台/元) |
A | B | 出发地 目的地 机器(台) |
A | B | 合计 | |
| 甲 | 500 | 300 | 甲地 | x | 15 | ||
| 乙 | 400 | 600 | 乙地 | 13 | |||
| 合计 | 16 | 12 | 28 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com