
【题目】(2016青海省西宁市)如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
A. B.
B.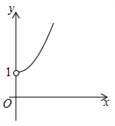 C.
C.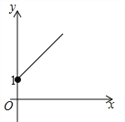 D.
D.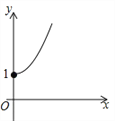
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
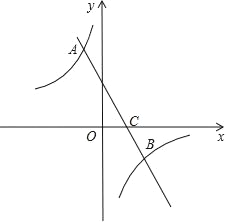
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
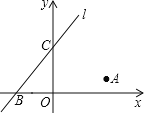
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,当
,当![]() 轴上的动点
轴上的动点![]() 到直线
到直线![]() 的距离
的距离![]() 与到点
与到点![]() 的距离
的距离![]() 之和最小时,则点
之和最小时,则点![]() 的坐标是__________.
的坐标是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
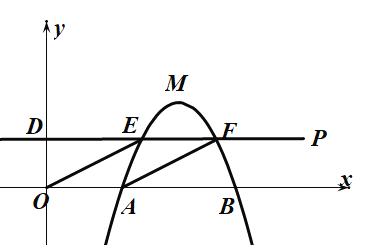
【题目】已知二次函数y=﹣x2+bx+c的图象经过点A(2,0),B(5,0),过点D(0,![]() )作y轴的垂线DP交图象于E、F.
)作y轴的垂线DP交图象于E、F.
(1)求b、c的值和抛物线的顶点M的坐标;
(2)求证:四边形OAFE是平行四边形;
(3)将抛物线向左平移的过程中,抛物线的顶点记为M′,直线DP与抛物线的左交点为E′,连接OM′,OE′,当OE′+OM′的值最小时求直线OE′的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
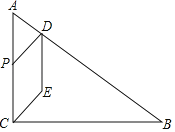
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,点D为AB边上一点,且AD=1,点P从点C出发,沿射线CA以每秒1个单位长度的速度运动,以CP、DP为邻边作CPDE.设CPDE和△ABC重叠部分图形的面积为S(平方单位),点P的运动时间为t(秒)(t>0)
(1)连结CD,求CD的长;
(2)当CPDE为菱形时,求t的值;
(3)求S与t之间的函数关系式;
(4)将线段CD沿直线CE翻折得到线段C′D′.当点D′落在△ABC的边上时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
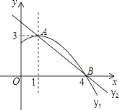
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把两块同样大小的含![]() 角的三角板的直角重合并按图1方式放置,点
角的三角板的直角重合并按图1方式放置,点![]() 是两块三角板的边
是两块三角板的边![]() 与
与![]() 的交点,将三角板
的交点,将三角板![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 到图2的位置,若
到图2的位置,若![]() ,则点
,则点![]() 所走过的路程是_________.
所走过的路程是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为x=![]() ,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )
,且经过点(2,0),有下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(0,y1),(1,y2)是抛物线上的两点,则y1=y2.上述说法正确的是( )

A.①②④ B.③④ C.①③④ D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
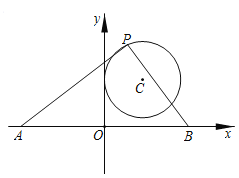
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com