
【题目】如图,在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+2S2+2S3+S4= .
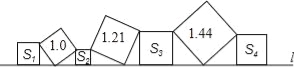
【答案】3.65
【解析】
试题分析:由条件可以得出AC=CF=1,FH=LH=1.1,PR=SR=1.2.由正方形的性质可以得出∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,就可以得出△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,就可以得出AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST,由勾股定理就可以AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2,由正方形的面积公式就可以得出结论.
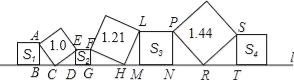
试题解析:如图, ∵斜放置的三个正方形的面积分别为1,1.21,1.44,
∴AC=CF=1,FH=LH=1.1,PR=SR=1.2.∠ACD=∠FHL=∠PRS=90°,
∴∠ACB=∠CED,∠FHG=∠HLM,∠PRN=∠RST,
∴△ABC≌△CDE,△FGH≌△HML,△PNR≌△RTS,
∴AB=CD,BC=DE,FG=HM,GH=ML,PN=RT,NR=ST, 由勾股定理,得
AB2+BC2=AC2,FG2+GH2=FH2,NP2+NR2=PR2, ∴S1+S2=1.0,S2+S3=1.21,S3+S4=1.44,
∴S1+S2+S2+S3+S3+S4=1+1.21+1.44=3.65, ∴S1+2S2+2S3+S4=3.65.


科目:初中数学 来源: 题型:
【题目】在△ABC和△DEF中,∠A=∠D=90°,则下列条件中不能判定△ABC和△DEF全等的是( )
A.AB=DE,AC=DF
B.AC=EF,BC=DF
C.AB=DE,BC=EF
D.∠C=∠F,BC=EF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中错误的命题是( )
A. (﹣3)2的平方根是±3
B. 平行四边形是中心对称图形
C. 单项式5x2y与﹣5xy2是同类项
D. 近似数3.14×103有三个有效数字
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
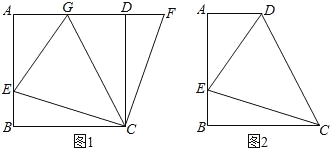
(1)求证:CE=CF;
(2)在图1中,若G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图2,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC=24,E是AB上一点,且∠DCE=45°,BE=8,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=2x2﹣12x+16绕它的顶点旋转180°,所得抛物线的解析式是( )
A. y=﹣2x2﹣12x+16 B. y=﹣2x2+12x﹣16
C. y=﹣2x2+12x﹣20 D. y=﹣2x2+12x﹣19
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. x4·x4=x16 B. (a3)2·a4=a9 C. (ab2)3÷(-ab)2=-ab4 D. (a6)2÷(a4)3=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是随机事件的是( )
A. 掷一次骰子,在骰子向上的一面上的点数大于0
B. 掷一次骰子,在骰子向上的一面上的点数为7
C. 掷三次骰子,在骰子向上的一面上的点数之和刚好为18
D. 掷两次骰子,在骰子向上的一面上的点数之积刚好是11
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com