
【题目】如图,在四边形BCED中,∠D=E=90°,A是DE上一点,且AB⊥AC,,AB=AC,若BD=4cm,CE=3cm, (1)说明DE、BD、EC三者之间存在怎样的数量关系?(2)求![]() 的面积。
的面积。

【答案】(1)DE=BD+CE,理由见解析;(2)12.5
【解析】试题分析:(1)根据AAS得到△ABD≌△CAE,得出AD=EC,BD=AE,从而推出DE=BD+CE;
(2)根据勾股定理求得AB的长度,再求三角形的面积.
试题解析:
∵∠D=90°,
∴∠DBA+∠BAD=90°,
又∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∴∠DBA=∠CAE(同角的余角相等),
在△DBA和△EAC中
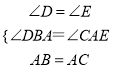 ,
,
∴△DBA≌△EAC(AAS),
∴AD=EC,BD=AE,
又∵DE=DA+AE,
∴DE=BD+CE;
(2)∵AD=EC,CE=3cm,
∴AD=3,
在Rt△ABD中,BD=4cm,
∴AB=![]() cm,
cm,
又∵AB=AC,
∴AC=5cm,
∴S△ABC=![]() cm2.
cm2.


科目:初中数学 来源: 题型:
【题目】如图,在方格纸中(小正方形的边长为1),△ABC的三个顶点均为格点,将△ABC沿x轴向左平移5个单位长度,根据所给的直角坐标系(O是坐标原点),解答下列问题:

(1)画出平移后的△A′B′C′,并直接写出点A′、B′、C′的坐标;
(2)求出在整个平移过程中,△ABC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(3a2b-2a2b)-(ab-4a2)+(2ab-a2b),其中a=-2,b=-3;
(2)3xy2-2![]() +(3x2y-2xy2),其中x=-4,y=
+(3x2y-2xy2),其中x=-4,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面不正确的是()
A. 数轴是一条规定了原点,正方向和长度单位的射线 B. 离原点近的点所对应的有理数较小
C. 数轴可以表示任意有理数 D. 原点在数轴的正中间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com