
【题目】定义:有一个角是其对角两倍的圆的内接四边形叫做圆美四边形,其中这个角叫做美角![]() 已知四边形ABCD是圆美四边形
已知四边形ABCD是圆美四边形
![]() 求美角
求美角![]() 的度数;
的度数;
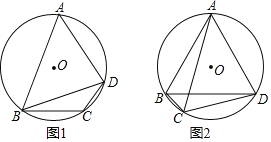
![]() 如图1,若
如图1,若![]() 的半径为
的半径为![]() ,求BD的长;
,求BD的长;
![]() 如图2,若CA平分
如图2,若CA平分![]() ,求证:
,求证:![]() .
.
 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
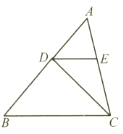
【题目】如图,在△ABC 中,AB=4,D 是 AB 上的一点(不与点 A、B 重合),DE∥BC,交AC 于点 E.设△ABC 的面积为 S,△DEC 的面积为 S'.
(1)当D是AB中点时,求![]() 的值;
的值;
(2)设AD=x,![]() =y,求y与x的函数表达式,并写出自变量x的取值范围;
=y,求y与x的函数表达式,并写出自变量x的取值范围;
(3)根据y的范围,求S-4S′的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
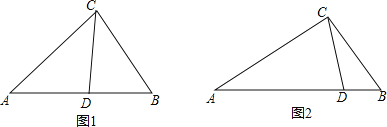
![]() 如图1,在
如图1,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() ,求证:CD为
,求证:CD为![]() 的完美分割线.
的完美分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 为等腰三角形,求
为等腰三角形,求![]() 的度数.
的度数.
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 是以CD为底边的等腰三角形,求完美分割线CD的长.
是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BC为⊙O的弦,点A为⊙O上一个动点,△OBC的周长为16.过C作CD∥AB交⊙O于D,BD与AC相交于点P,过点P作PQ∥AB交于Q,设∠A的度数为α.
(1)如图1,求∠COB的度数(用含α的式子表示);
(2)如图2,若∠ABC=90°时,AB=8,求阴影部分面积(用含α的式子表示);
(3)如图1,当PQ=2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,![]() ,
,![]() ,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为
,以点A为旋转中心,逆时针旋转矩形ABCD,旋转角为![]() ,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
,得到矩形AEFG,点B、点C、点D的对应点分别为点E、点F、点G.
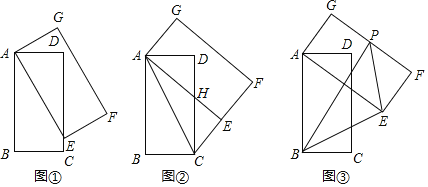
![]() 如图
如图![]() ,当点E落在DC边上时,直写出线段EC的长度为______;
,当点E落在DC边上时,直写出线段EC的长度为______;
![]() 如图
如图![]() ,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
,当点E落在线段CF上时,AE与DC相交于点H,连接AC,
![]() 求证:
求证:![]() ≌
≌![]() ;
;
![]() 直接写出线段DH的长度为______.
直接写出线段DH的长度为______.
![]() 如图
如图![]() 设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,
设点P为边FG的中点,连接PB,PE,在矩形ABCD旋转过程中,![]() 的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
的面积是否存在最大值?若存在请直接写出这个最大值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠BAC=90°,AB=AC=2![]() ,圆A的半径1,点O在BC边上运动(与点B/C不重合),设BO=X,△AOC的面积是y.
,圆A的半径1,点O在BC边上运动(与点B/C不重合),设BO=X,△AOC的面积是y.
⑴求y关于x的函数关系式及自变量的取值范围;
⑵以点O位圆心,BO为半径作圆O,求当○O与○A相切时,△AOC的面积.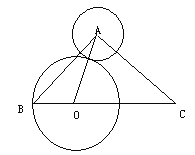
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
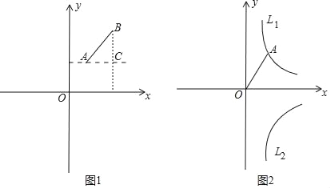
如图(1),在平面直角坐标系xOy中,已知点A的坐标是(1,2),点B的坐标是(3,4),过点A、点B作平行于x轴、y轴的直线相交于点C,得到Rt△ABC,由勾股定理可得,线段AB=![]() .
.
得出结论:
(1)若A点的坐标为(x1,y1),B点的坐标为(x2,y2)请你直接用A、B两点的坐标表示A、B两点间的距离;
应用结论:
(2)若点P在y轴上运动,试求当PA=PB时,点P的坐标.
(3)如图(2)若双曲线L1:y=![]() (x>0)经过A(1,2)点,将线段OA绕点O旋转,使点A恰好落在双曲线L2:y=﹣
(x>0)经过A(1,2)点,将线段OA绕点O旋转,使点A恰好落在双曲线L2:y=﹣![]() (x>0)上的点D处,试求A、D两点间的距离.
(x>0)上的点D处,试求A、D两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
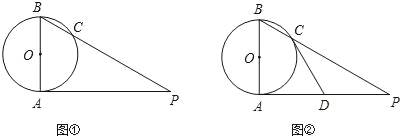
【题目】已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C。
(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2016年国庆后,许多高校均投放了使用手机就可随用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费作如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5(含5次以上) |
累计车费 | 0 | 0.5 | 0.9 |
|
| 1.5 |
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 5 | 15 | 10 | 30 | 25 | 15 |
(Ⅰ)写出![]() 的值;
的值;
(Ⅱ)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利? 说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com