
【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元?
【答案】
(1)解:设第一批衬衫每件进价是x元,则第二批每件进价是(x﹣10)元,根据题意可得: ![]() ,
,
解得:x=150,
经检验x=150是原方程的解,
第一批衬衫每件进价是150元,第二批每件进价是140元,
![]() (件),
(件), ![]() (件),
(件),
答:第一批衬衫进了30件,第二批进了15件
(2)解:设第二批衬衫每件售价y元,根据题意可得:
30×(200﹣150)+15(y﹣140)≥1950,
解得:y≥170,
答:第二批衬衫每件至少要售170元
【解析】根据题意列出分式方程,设第一批衬衫每件进价是x元,则第二批每件进价是(x﹣10)元,根据题意可得![]() ,解得:x=150,得到第一批衬衫每件进价是150元,第二批每件进价是140元,求出这两次各购进这种衬衫数件;(2)设第二批衬衫每件售价y元,根据题意可得:30×(200﹣150)+15(y﹣140)≥1950,解得:y≥170,所以第二批衬衫每件至少要售170元.
,解得:x=150,得到第一批衬衫每件进价是150元,第二批每件进价是140元,求出这两次各购进这种衬衫数件;(2)设第二批衬衫每件售价y元,根据题意可得:30×(200﹣150)+15(y﹣140)≥1950,解得:y≥170,所以第二批衬衫每件至少要售170元.
【考点精析】利用分式方程的应用对题目进行判断即可得到答案,需要熟知列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位).


科目:初中数学 来源: 题型:
【题目】操作与探究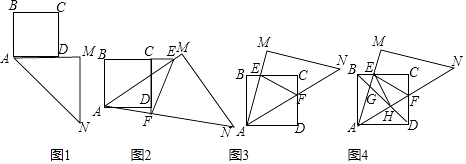
综合实践课,老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧,使边AM与AD在同
一直线上(如图1),其中∠AMN=90°,AM=MN.
(1)猜想发现
老师将三角尺AMN绕点A逆时针旋转α.如图2,当0<α<45°时,边AM,AN分别与直线BC,CD交于点E,F,连结EF.小明同学探究发现,线段EF,BE,DF满足EF=BE﹣DF;如图3,当45°<α<90°时,其它条件不变.
①填空:∠DAF+∠BAE=度;
②猜想:线段EF,BE,DF三者之间的数量关系是: .
(2)证明你的猜想;
(3)拓展探究
在45°<α<90°的情形下,连结BD,分别交AM,AN于点G,H,如图4连结EH,试证明:EH⊥AN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连接EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.

(1)求证:OE=OF;
(2)如图(2),若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其他条件不变,则结论“OE=OF”还成立吗?如果成立,请给出证明;如果不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格中,每个小方格都是边长为1个单位长度的正方形,![]() 的三个顶点都在格点(小方格的顶点)上.
的三个顶点都在格点(小方格的顶点)上.
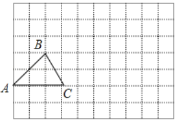
(1)请建立适当的平面直角坐标系,使![]() ,
,![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)在(1)的条件下,将![]() 先向右平移4个单位长度再向上平移2个单位长度后可得到
先向右平移4个单位长度再向上平移2个单位长度后可得到![]() ,请在图中画出平移后的
,请在图中画出平移后的![]() ,并分别写出点
,并分别写出点![]() ,
,![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
科目:初中数学 来源: 题型:
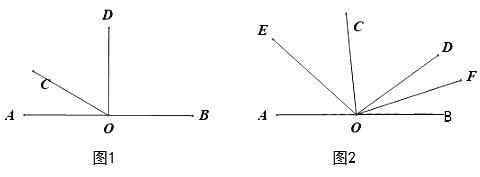
【题目】如图1,点O是直线AB上的一点.
(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;
(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;
(3)在(1)中线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当OD与OB重合时旋转都停止),OM、ON分别平分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
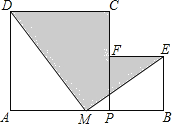
【题目】如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连结MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com