练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】多项式3a2-ab3+18的次数是____________．

    【答案】4

    【解析】

    根据多项式次数的定义求解．多项式的次数是多项式中最高次项的次数．

    依题意知，此题的最高次项是-ab3，

    则多项式的次数是4．

    故答案为：4．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

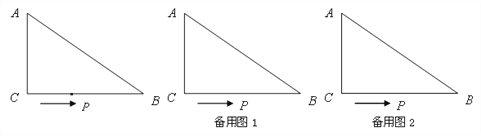
    【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径，以2cm每秒的速度运动，设运动时间为t秒.

    (1) 当t=1时，求△ACP的面积

    (2) t为何值时，线段AP是∠CAB的平分线？

    (3) 请利用备用图2继续探索：当t为何值时，△ACP是以AC为腰的等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

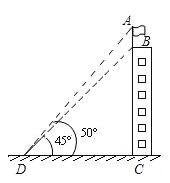
    【题目】测量计算是日常生活中常见的问题，如图，建筑物BC的屋顶有一根旗杆AB，从地面上D点处观测旗杆顶点A的仰角为50°，观测旗杆底部B点的仰角为45°，（可用的参考数据：sin50°≈0.8，tan50°≈1.2）

    （1）若已知CD=20米，求建筑物BC的高度；（2）若已知旗杆的高度AB=5米，求建筑物BC的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

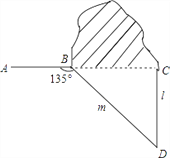
    【题目】如图，修公路遇到一座山，于是要修一条隧道．为了加快施工进度，想在小山的另一侧同时施工．为了使山的另一侧的开挖点C在AB的延长线上，设想过C点作直线AB的垂线L，过点B作一直线（在山的旁边经过），与L相交于D点，经测量∠ABD=135°，BD=800米，求直线L上距离D点多远的C处开挖？（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

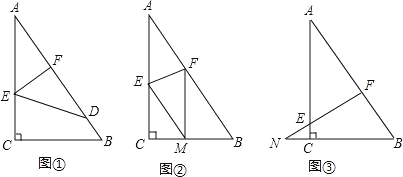
    【题目】如图，已知一个直角三角形纸片ACB，其中∠ACB=90°，AC=4，BC=3，E、F分别是AC、AB边上点，连接EF．

    （1）图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF=3S△EDF，求AE的长；

    （2）如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M处，且使MF∥CA．

    ①试判断四边形AEMF的形状，并证明你的结论；

    ②求EF的长；

    （3）如图③，若FE的延长线与BC的延长线交于点N，CN=1，CE=，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

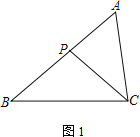
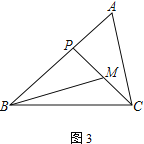
    【题目】在△ABC中，P为边AB上一点．

    (1) 如图1，若∠ACP＝∠B，求证：AC2＝AP·AB；

    (2) 若M为CP的中点，AC＝2，

    ① 如图2，若∠PBM＝∠ACP，AB＝3，求BP的长；

    ② 如图3，若∠ABC＝45°，∠A＝∠BMP＝60°，直接写出BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

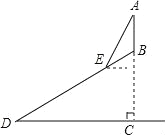
    【题目】某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度，已知烈山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于平面直角坐标系中的任意两点我们把叫做、两点间的直角距离.

    （1）已知点A（1,1），点B（3,4），则d（A，B）=________.

    （2）已知点E（a,a），点F（2,2），且d（E，F）=4，则a=________.

    （3）已知点M（m,2）点N（1,0），则d（M,N）的最小值为________.

    （4）设是一定点，Q（x,y）是直线y=ax+b上的动点，我们把d（，Q）的最小值叫做到直线y=ax+b的直角距离，试求点M（5,1）到直线y=x+2的直角距离.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

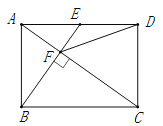
    【题目】如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，分析下列四个结论：①△AEF∽△CAB；②CF＝2AF；③DF＝DC；④tan∠CAD＝．其中正确的结论有( )

    A.4个 B．3个 C．2个 D．1个

    查看答案和解析>>

    同步练习册答案