考点:质数与合数
专题:
分析:采用反证法.假设存在一个十进制的质数
,使得b
2-4ac为平方数.分别得到f(x)=ax
2+bx+c=0①.已知条件意味着 p=f(10)=a×10
2+b×10+c=
是一个质数方程①的两个根x=
②,取x=10,得p=a(10-x
1)(10-x
2)③.将式两边同乘以4a得 4ap=(20a-2ax
1)(20a-2ax
2)④.结合式④,导出|20a-2ax
2|≤4a⑤.由式②易知x
2≤0.从而,式⑤不可能成立,矛盾.
解答:证明:采用反证法.
假设存在一个十进制的质数
,使得b
2-4ac为平方数.注意到求证结果的形式,可考虑(辅助的)二次方程
f(x)=ax
2+bx+c=0①.
已知条件意味着 p=f(10)=a×10
2+b×10+c=
是一个质数.
由于b
2-4ac是完全平方数,
故方程①的两个根x=
②
均为有理数.于是,
ax
2+bx+c=a(x-x
1)(x-x
2).
取x=10,
得p=a(10-x
1)(10-x
2)③.
由式②可知2ax
1、2ax
2均是整数.
将式两边同乘以4a得 4ap=(20a-2ax
1)(20a-2ax
2)④.
因p是质数,所以,式④右边的两个因子中必有一个被p整除,不妨设20a-2ax
1是p的倍数.
注意到20a-2ax
1≠0,
故|20a-2ax
1|≥p.
结合式④,导出|20a-2ax
2|≤4a⑤.
但由式②易知x
2≤0.
从而,式⑤不可能成立,矛盾.
点评:考查了质数与合数,当题目条件中出现形如b2-4ac一类平方与积的差的形式的式子时常利用判别式构造方程.



 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案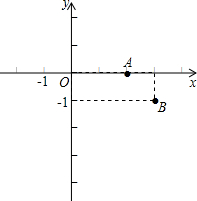 如图,在平面直角坐标系xOy中,点A、B的坐标分别为(2,0)、(3,-1),二次函数y=-x2的图象为C1.
如图,在平面直角坐标系xOy中,点A、B的坐标分别为(2,0)、(3,-1),二次函数y=-x2的图象为C1.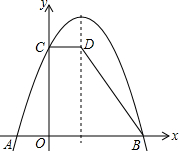 已知:如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D.
已知:如图,抛物线y=-x2+bx+c与x轴交于点A(-1,0),B(3,0),与y轴交于点C.过点C作CD∥x轴,交抛物线的对称轴于点D. 已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )
已知,如图,点C、D在⊙O上,直径AB=6cm,弦AC、BD相交于点E.若CE=BC,则阴影部分面积为( )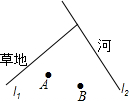 如图,牧区内有一家牧民,点A处有一个马厩,点B处是他的家.l1是草地的边沿,l2是一条笔直的河流.每天,牧民要从马厩牵出马来,先去草地上让马吃草,再到河边饮马,然后回到家B处.请在图上画出牧民行走的最短路线(保留作图痕迹).
如图,牧区内有一家牧民,点A处有一个马厩,点B处是他的家.l1是草地的边沿,l2是一条笔直的河流.每天,牧民要从马厩牵出马来,先去草地上让马吃草,再到河边饮马,然后回到家B处.请在图上画出牧民行走的最短路线(保留作图痕迹).