
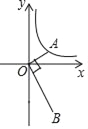
【题目】如图,已知点A是反比例y=![]() (x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
(x>0)的图象上的一个动点,连接OA,OB⊥OA,且OB=2OA,那么经过点B的反比例函数图象的表达式为_____.
【答案】y=-![]()
【解析】
过A作AC⊥y轴,BD⊥y轴,可得∠ACO=∠BDO=90°,利用三角关系得到三角形相似,由相似得比例求出相似比,确定出面积比,求出三角形AOC面积,进而确定出三角形OBD面积,利用反比例函数k的几何意义确定出所求k的值,即可确定出解析式.
过A作AC⊥y轴,BD⊥y轴,可得∠ACO=∠BDO=90°.
∵∠AOC+∠OAC=90°,∠AOC+∠BOD=90°,∴∠OAC=∠BOD,∴△AOC∽△OBD.
∵OB=2OA,∴△AOC与△OBD相似比为1:2,∴S△AOC:S△OBD=1:4.
∵点A在反比例y=![]() 上,∴△AOC面积为
上,∴△AOC面积为![]() ,∴△OBD面积为2,即k=4,则点B所在的反比例解析式为y=﹣
,∴△OBD面积为2,即k=4,则点B所在的反比例解析式为y=﹣![]() .
.
故答案为:y=﹣![]() .
.


 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案科目:初中数学 来源: 题型:
【题目】某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
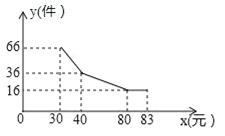
(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+3的图象过点A(-1,0),对称轴为过点(1,0)且与y轴平行的直线.
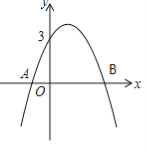
(1)求点B的坐标
(2)求该二次函数的关系式;
(3)结合图象,解答下列问题:
①当x取什么值时,该函数的图象在x轴上方?
②当-1<x<2时,求函数y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校教师开展了“练一手好字”的活动,校委会对部分教师练习字帖的情况进行了问卷调查,问卷设置了“柳体”、“颜体”、”欧体“和”其他“类型,每位教师仅能选一项,根据调查的结果绘制了如下统计表:
类别 | 柳体 | 颜体 | 欧体 | 其他 | 合计 |
人数 | 4 | 10 | 6 | ||
占的百分比 | 0.5 | 0.25 | 1 |
根据图表提供的信息解答下列问题:
(1)这次问卷调查了多少名教师?
(2)请你补全表格.
(3)在调查问卷中,甲、乙、丙、丁四位教师选择了“柳体”,现从以上四位教师中任意选出2名教师参加学校的柳体兴趣小组,请你用画树状图或列表的方法,求选出的2人恰好是乙和丙两位教师的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场一种商品的进价为每件30元,售价为每件40元.每天可以销售48件,为尽快减少库存,商场决定降价促销.
(1)若该商品连续两次下调相同的百分率后售价降至每件32.4元,求两次下降的百分率;
(2)经调查,若每降价0.5元,每天可多销售4件,那么每天要想获得510元的利润,每件应降价多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元![]() ,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式(不要求写自变量的取值范围);
(2)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,E、F是对角线AC上两点,连接BE、BF、DE、DF,则添加下列条件①∠ABE=∠CBF;②AE=CF;③AB=AF;④BE=BF.可以判定四边形BEDF是菱形的条件有( )
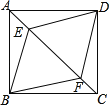
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
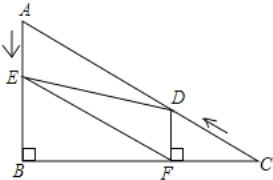
【题目】 如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点D从点C出发沿
.点D从点C出发沿![]() 方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿
方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿![]() 方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒
方向以每秒2个单位长的速度向点B匀速运动,设点D、E运动的时间是t秒![]() .过点D作
.过点D作![]() 于点F,连接
于点F,连接![]() 、
、![]() .
.
(1)求证:![]() ;
;
(2)四边形![]() 能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com