
 探索题
探索题 (1)猜想AC、AD、AE之间的关系为:AC=AD+AE,
(1)猜想AC、AD、AE之间的关系为:AC=AD+AE,
|
|


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:三维目标导学与测评·数学(北师大版)七年级上册 题型:059
探索题:
已知:如图,点C在线段AB上,线段AC=6cm,BC=4cm,点M,N分别是AC,BC的中点
(1)求:线段MN的长
(2)根据(1)的过程和结果,设AC+BC=a,其他条件不变,你能猜出MN的长吗?为什么?请用一句话表述你发现的规律
查看答案和解析>>
科目:初中数学 来源: 题型:
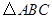 中,
中,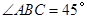 ,
,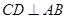 于
于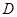 ,
,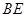 平分
平分 ,且
,且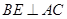 于
于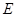 ,与
,与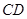 相交于点
相交于点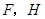 是
是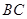 边的中点,连结
边的中点,连结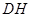 与
与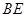 相交于点
相交于点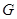 .
.
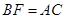 ;
;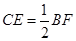 ;
; ,
,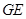 ,
,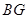 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州西兴中学八年级上学期期中考试数学卷 题型:解答题
已知:如图, 中,
中, ,
, 于
于 ,
,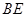 平分
平分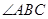 ,且
,且 于
于 ,与
,与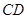 相交于点
相交于点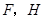 是
是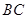 边的中点,连结
边的中点,连结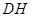 与
与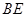 相交于点
相交于点 .
.
【小题1】求证: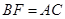 ;
;
【小题2】求证: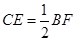 ;
;
【小题3】试探索 ,
, ,
,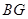 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省杭州市萧山瓜沥片八年级12月月考数学卷 题型:解答题
已知:如图,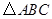 中,
中,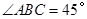 ,
, 于
于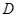 ,
,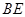 平分
平分 ,且
,且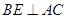 于
于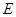 ,与
,与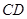 相交于点
相交于点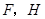 是
是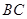 边的中点,连结
边的中点,连结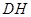 与
与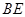 相交于点
相交于点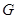 .
.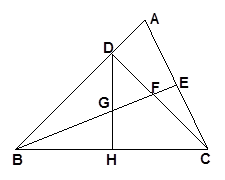
【小题1】(1)说明: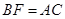 ;
;
【小题2】(2)说明: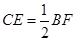 ;
;
【小题3】(3)试探索 ,
,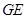 ,
, 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com