练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

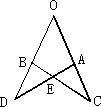
    如图，OC＝OD，若要使△OAD≌△OBC，则还需要添加的一个条件是________．

    答案：
    解析：

    答案不唯一，如OA＝OB或∠C＝∠D等


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：中华题王　数学　九年级上　(北师大版) 北师大版 题型：047

    如图，已知AD、BC相交于O．

    (1)给出下列条件：①∠C＝∠D；②OC＝OD；③OB＝OA；④AC＝BD．以上四个条件由哪两个条件组合(不添加辅助线)就可以判别△ABC≌△BAD？请你任选一种组合．进行证明．

    (2)图中，若∠C＝∠D＝90°，试在AB上找一点P，使PC＝PD，写出P点应满足的条件，并给出证明或说明理由．

    查看答案和解析>>

    科目：初中数学 来源：2013年北京市门头沟区中考二模数学试卷（带解析） 题型：解答题

    已知：在△AOB与△COD中，OA＝OB，OC＝OD，．
    （1）如图1，点C、D分别在边OA、OB上，连结AD、BC，点M为线段BC的中点，连结OM，则线段AD与OM之间的数量关系是                         ，位置关系是                    ；

    （2）如图2，将图1中的△COD绕点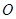逆时针旋转，旋转角为 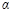(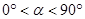)．连结AD、BC，点M为线段BC的中点，连结OM．请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由；

    （3）如图3，将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与△AOB的边OA在同一条直线上时，点C落在OB上，点M为线段BC的中点．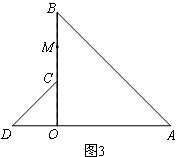

    请你判断（1）中线段AD与OM之间的数量关系是否发生变化，写出你的猜想，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源：2013年北京市门头沟区中考二模数学试卷（解析版） 题型：解答题

    已知：在△AOB与△COD中，OA＝OB，OC＝OD，．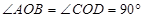

    （1）如图1，点C、D分别在边OA、OB上，连结AD、BC，点M为线段BC的中点，连结OM，则线段AD与OM之间的数量关系是                         ，位置关系是                    ；

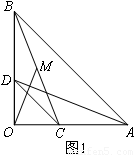
    （2）如图2，将图1中的△COD绕点逆时针旋转，旋转角为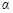 (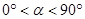)．连结AD、BC，点M为线段BC的中点，连结OM．请你判断（1）中的两个结论是否仍然成立．若成立，请证明；若不成立，请说明理由；

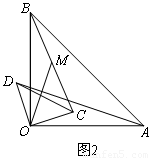
    （3）如图3，将图1中的 △COD绕点 O逆时针旋转到使 △COD的一边OD恰好与△AOB的边OA在同一条直线上时，点C落在OB上，点M为线段BC的中点．

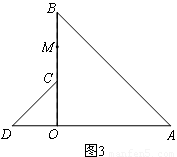
    请你判断（1）中线段AD与OM之间的数量关系是否发生变化，写出你的猜想，并加以证明．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

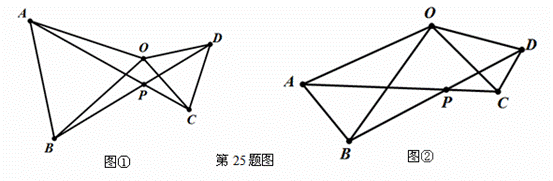
    已知：在△AOB和△COD中，OA＝OB，OC＝OD。

    （1）如图①，若∠AOB＝∠COD＝60º，

         求证：①AC＝BD ；  ②∠APB＝60º.

    （2）如图②，若∠AOB＝∠COD＝，则AC与BD间的等量关系式为______________，

    ∠APB的大小为__________（直接写出结果，不证明）

    查看答案和解析>>

    同步练习册答案