
 如图△ABC中,边BC=60,高AD=40,EFGH是内接矩形,HG交AD于P,设HE=x,
如图△ABC中,边BC=60,高AD=40,EFGH是内接矩形,HG交AD于P,设HE=x, =
= ,即
,即 =
=
 (40-x),
(40-x), (40-x)=2x+120-3x=120-x(0<x<40);
(40-x)=2x+120-3x=120-x(0<x<40); (40-x)=-
(40-x)=- x2+60x(0<x<40).
x2+60x(0<x<40). (40-x),然后根据矩形的周长确定y与x的关系;
(40-x),然后根据矩形的周长确定y与x的关系;

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
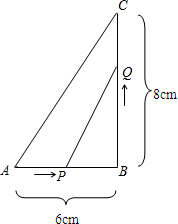 开始沿BC边向点C以2cm/s的速度匀速移动.
开始沿BC边向点C以2cm/s的速度匀速移动.查看答案和解析>>
科目:初中数学 来源: 题型:
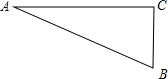 ,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?
,BC=1,AB=2,连接AC,那么得到的△ABC是否是直角三角形呢?画完后他发现是的,你能帮他证明吗?查看答案和解析>>
科目:初中数学 来源: 题型:
 如图△ABC中,边BC=60,高AD=40,EFGH是内接矩形,HG交AD于P,设HE=x,
如图△ABC中,边BC=60,高AD=40,EFGH是内接矩形,HG交AD于P,设HE=x,查看答案和解析>>
科目:初中数学 来源: 题型:
 已知如图△ABC放置于边长为1的小正方形组成的网格中中,AB=
已知如图△ABC放置于边长为1的小正方形组成的网格中中,AB=| 2 |
| 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com