练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．已知tanα=$\frac{\sqrt{3}}{2}$，则sinα=±$\frac{2\sqrt{21}}{14}$．

    分析 由tanα的值，利用同角三角函数间的基本关系求出cosα的值，进而求出sinα的值．

    解答 解：∵tanα=$\frac{\sqrt{3}}{2}$，
    ∴cosα=±$\sqrt{\frac{1}{1+ta{n}^{2}α}}$=±$\frac{2\sqrt{7}}{7}$，
    ∴sinα=tanα•cosα=$\frac{\sqrt{3}}{2}$×（±$\frac{2\sqrt{7}}{7}$）=±$\frac{2\sqrt{21}}{14}$．
    故答案是：±$\frac{2\sqrt{21}}{14}$．

    点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    13．如图，在平面直角坐标系xOy中，抛物线y=x2+（5k+1）x+5k （5k＞1）与x轴交于点A、B，与y轴交于点C，点D在坐标平面内，AD⊥BC，OD=5，点E在抛物线上，OD⊥OE，OD=OE，
    （1）求抛物线解析式；
    （2）过点C作直线l∥x轴，x轴上有一个动点F，过F作FM⊥BC、FN⊥直线l，分别交线段BC、直线l于点M、N，设△CMN的面积为S，点F的横坐标为t，求S与t之间的函数关系式，并写出相应的自变量t的取值范围．
    （3）在（2）的条件下，当点F在x轴正半轴时，将∠MFN绕点F顺时针旋转30°，角的两边分别交射线BC和直线l于点P、Q，当PF平分∠BPQ时，求F点坐标．

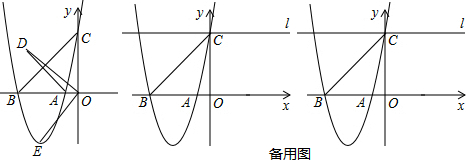
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．下列各式：$\sqrt{{x}^{2}+1}$，$\sqrt{a-3}$（a≥3），$\sqrt{-（{b}^{2}+3）^{2}}$，$\sqrt{（\frac{y}{4}）^{2}}$中属于二次根式的共有（　　）
    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．化简：$\frac{x-1}{x+2}$÷$\frac{{x}^{2}-2x+1}{{x}^{2}-4}$=$\frac{x-2}{x-1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．如果x+y=5，x2+y2=21，那么（x-y）2=17．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．若a＜0，且|a|=2，则a+1=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

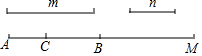    15．如图所示，已知线段m＞n，求作一线段m-n．作法：画射线AM，在射线AM上截取AB=m，在线段AB上截取BC=n，那么所求的线段是（　　）
    A．ACB．BCC．ABD．BM

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图1，在△ABC中，AB=AC，点E是BC上一点，点D是AE上一点，且∠BDE=∠BAC，CF∥BD，交AE的延长线于点F．
    （1）探究线段AD与CF的数量关系．
    （2）若将“AB=AC，点E是BC上一点，点D是AE上一点”改为“AB=kAC，点E是BC延长线上一点，点D是EA延长线上一点”，其他条件不变，如图2，若AD=n，AF=m，∠BAC=α，求BD的长（用含m，n，k，α的式子表示）

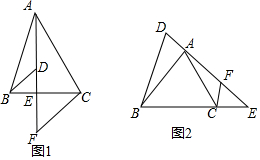
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

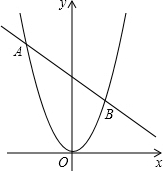    13．如图，已知直线AB：y=kx+2k+4与抛物线y=$\frac{1}{2}$x2交于A、B两点．
    （1）直线AB总经过一个定点C，请直接写出点C坐标；
    （2）当k=-$\frac{1}{2}$时，在直线AB下方的抛物线上求点P，使△ABP的面积等于5．

    查看答案和解析>>

    同步练习册答案