
【题目】关于![]() 的二次函数y=x2+2kx+k-1,下列说法正确的是( )
的二次函数y=x2+2kx+k-1,下列说法正确的是( )
A. 对任意实数k,函数与x轴都没有交点
B. 存在实数n,满足当![]() 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小
C. 不存在实数n,满足当![]() 时,函数y的值都随x的增大而减小
时,函数y的值都随x的增大而减小
D. 对任意实数k,抛物线![]() 都必定经过唯一定点
都必定经过唯一定点
【答案】D
【解析】A、∵△=(2k)2﹣4(k﹣1)=4k2﹣4k+4=4(k﹣)2+3>0,∴抛物线的与x轴都有两个交点,故A错误;B、∵a=1>0,抛物线的对称轴x=﹣![]() =﹣k,∴在对称轴的左侧函数y的值都随x的增大而减小,即当x<k时,函数y的值都随x的增大而减小,当n=﹣k时,当x≥n时,函数y的值都随x的增大而增大,故B错误;C、由对称轴可知,当n=﹣k时,当x≤n时,函数y的值都随x的增大而减小,故C错误; D、令k=1和k=0,得到方程组:
=﹣k,∴在对称轴的左侧函数y的值都随x的增大而减小,即当x<k时,函数y的值都随x的增大而减小,当n=﹣k时,当x≥n时,函数y的值都随x的增大而增大,故B错误;C、由对称轴可知,当n=﹣k时,当x≤n时,函数y的值都随x的增大而减小,故C错误; D、令k=1和k=0,得到方程组: ![]() ,解得
,解得 ,将
,将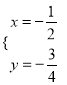 代入x2+2kx+k﹣1得,
代入x2+2kx+k﹣1得, ![]() ﹣k+k﹣1=﹣
﹣k+k﹣1=﹣![]() ,与k值无关,不论k取何值,抛物线总是经过一个定点(﹣
,与k值无关,不论k取何值,抛物线总是经过一个定点(﹣![]() ,﹣
,﹣![]() ),故D正确.故选D.
),故D正确.故选D.


科目:初中数学 来源: 题型:
【题目】如图,在一正方形ABCD中.E为对角线AC上一点,连接EB、ED,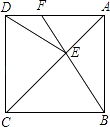
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有Rt△ABC,∠BAC=90°,AB=AC,A(﹣3,0),B(0,1),C(m,n).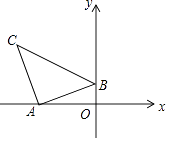
(1)请直接写出C点坐标.
(2)将△ABC沿x轴的正方向平移t个单位,B′、C′两点的对应点、正好落在反比例函数y= ![]() 在第一象限内图象上.请求出t,k的值.
在第一象限内图象上.请求出t,k的值.
(3)在(2)的条件下,问是否存x轴上的点M和反比例函数y= ![]() 图象上的点N,使得以B′、C′,M,N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
图象上的点N,使得以B′、C′,M,N为顶点的四边形构成平行四边形?如果存在,请求出所有满足条件的点M和点N的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w![]() (千克)随销售单价x
(千克)随销售单价x![]() (元/千克)的变化而变化,具体关系式为
(元/千克)的变化而变化,具体关系式为![]() ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为![]() y(元),解答下列问题:
y(元),解答下列问题:
(1)求y![]() 与x
与x![]() 的关系式.
的关系式.
(2)当![]() x取何值时,
x取何值时,![]() y的值最大?
y的值最大?
(3)如果公司想要在这段时间内获得![]() 元的销售利润,销售单价应定为多少元?
元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com