
【题目】(本小题满分8分)已知:如图,△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE;垂足为E.
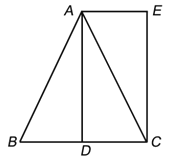
(1)求证:△ABD≌△CAE;
(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.
【答案】见解析;AB∥DE且AB=DE.
【解析】
试题(1)运用AAS证明△ABD≌△CAE;
(2)易证四边形ADCE是矩形,所以AC=DE=AB,也可证四边形ABDE是平行四边形得到AB=DE.
试题解析:证明:(1)∵AB=AC,
∴∠B=∠ACD,
∵AE∥BC,
∴∠EAC=∠ACD,
∴∠B=∠EAC,
∵AD是BC边上的中线,
∴AD⊥BC,
∵CE⊥AE,
∴∠ADC=∠CEA=90°
在△ABD和△CAE中
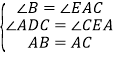
∴△ABD≌△CAE(AAS);
(2)AB∥DE,AB=DE,理由如下:
如图所示,
∵AD⊥BC,AE∥BC,
∴AD⊥AE,
又∵CE⊥AE,
∴四边形ADCE是矩形,
∴AC=DE,
∵AB=AC,
∴AB=DE,
∵AE∥BC,
∴四边形ABDE是平行四边形,
∴AB∥DE,AB=DE.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1, ![]() ≈1.73)
≈1.73)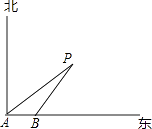
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:在△ABC中,AB、BC、AC三边的长分别为![]() 、
、![]() 、
、![]() ,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求此三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图①所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上: .
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.如果△ABC三边的长分别![]() a、
a、![]() a、
a、![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为2,OA与x轴负半轴的夹角为15°,点B在抛物线y=ax2(a<0)的图象上,则a的值为( )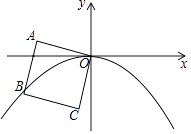
A.![]()
B.![]()
C.﹣2
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.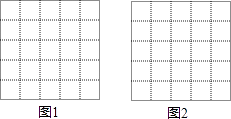
(1)在图1中画出钝角△ABC,使它的面积为6(画一个即可);
(2)在图2中画出△DEF,使它的三边长分别为 ![]() 、2
、2 ![]() 、5(画一个即可).并且直接写出此时三角形DEF的面积.
、5(画一个即可).并且直接写出此时三角形DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABDE、CDFI、EFGH的面积分别为25、9、16,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,则S1+S2+S3=_____.
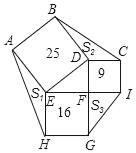
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠A=90°,点D是BC的中点,点E,F分别在AB,AC上,且∠EDF=90°,连接EF,求证:BE2+CF2=EF2.

查看答案和解析>>
科目:初中数学 来源: 题型:
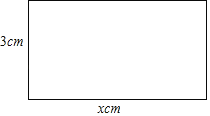
【题目】如图,已知长方形相邻两边的长分别是xcm和3cm,设长方形的面积为ycm2.
(1)试写出长方形的面积y与x之间的关系式;
(2)利用(1)中的关系式,求当x=5cm时长方形的面积;
(3)当x的值由4cm变化到12cm时,长方形的面积由 cm2变化到 cm2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com