
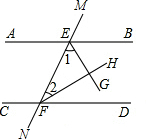
 如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?
如图,直线AB和CD被直线MN所截,EG平分∠BEF,FH平分∠DFE,问:当∠1与∠2互余时,AB与CD有什么位置关系?为什么?  全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:填空题
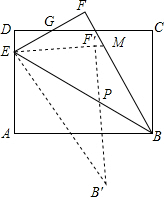 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
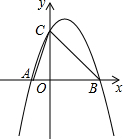 已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:
已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
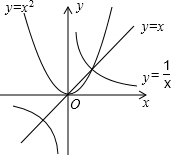 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:| A. | 正确的命题是①② | B. | 错误的命题是②③④ | C. | 正确的命题是①④ | D. | 错误的命题只有③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
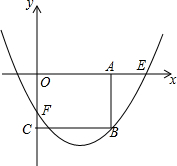 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com