
 �����������⼰����y=x��y=x2��y=$\frac{1}{x}$��ͼ��
�����������⼰����y=x��y=x2��y=$\frac{1}{x}$��ͼ��| A�� | ��ȷ�������Ǣ٢� | B�� | ����������Ǣڢۢ� | C�� | ��ȷ�������Ǣ٢� | D�� | ���������ֻ�Т� |
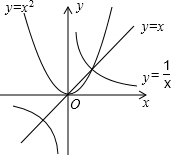
���� ��ȷ����������ͼ��Ľ�������Ϊ��1��1�����ٸ��ݶ��κ����벻��ʽ��Ĺ�ϵ��⼴�ɣ�
��� �⣺����x=1ʱ�����������ĺ���ֵ����1��
���ԣ���������Ϊ��1��1����
���ݶԳ��ԣ�y=x��y=$\frac{1}{x}$�ڵ������Ľ�������Ϊ��-1��-1����
�����$\frac{1}{a}$��a��a2����ô0��a��1���ʢ���ȷ��
�����a2��a��$\frac{1}{a}$����ôa��1��-1��a��0���ʢڴ���
�����$\frac{1}{a}$��a2��a����ôaֵ�����ڣ��ʢ۴���
�����a2��$\frac{1}{a}$��aʱ����ôa��-1���ʢ���ȷ��
������������ȷ�������Ǣ٢ܣ�����������Ǣڢۣ�
��ѡ��C��
���� ���⿼���˶��κ����벻��ʽ��Ĺ�ϵ�������붨�����������������꣬��ȷʶͼ�ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
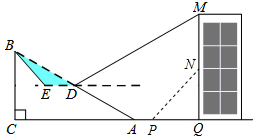 ��ͼ��б��AB��130�ף��¶�i=1��2.4��BC��AC���ּƻ���б���е�D����ȥ����������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��
��ͼ��б��AB��130�ף��¶�i=1��2.4��BC��AC���ּƻ���б���е�D����ȥ����������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
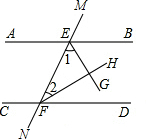 ��ͼ��ֱ��AB��CD��ֱ��MN���أ�EGƽ�֡�BEF��FHƽ�֡�DFE���ʣ�����1���2����ʱ��AB��CD��ʲôλ�ù�ϵ��Ϊʲô��
��ͼ��ֱ��AB��CD��ֱ��MN���أ�EGƽ�֡�BEF��FHƽ�֡�DFE���ʣ�����1���2����ʱ��AB��CD��ʲôλ�ù�ϵ��Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
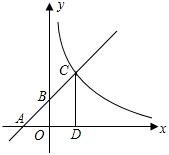 ��ͼ����֪һ�κ���y=kx+b��k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=$\frac{m}{x}$��x��0����ͼ���ڵ�һ�����ཻ�ڵ�C��CD��ֱ��x�ᣬ����Ϊ��D����OA=OB=2��OD=1��
��ͼ����֪һ�κ���y=kx+b��k��0����ͼ����x�ᡢy��ֱ���A��B���㣬���뷴��������y=$\frac{m}{x}$��x��0����ͼ���ڵ�һ�����ཻ�ڵ�C��CD��ֱ��x�ᣬ����Ϊ��D����OA=OB=2��OD=1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com