科目：初中数学 来源：2014-2015学年北京市昌平区九年级下学期第一次统一练习数学试卷（解析版） 题型：解答题
已知，点P是∠MON的平分线上的一动点，射线PA交射线OM于点A，将射线PA绕点P逆时针旋转交射线ON于点B，且使∠APB+∠MON=180°．
（1）利用图1，求证：PA=PB；
（2）如图2，若点
是
与
的交点，当
时，求PB与PC的比值；
（3）若∠MON=60°，OB=2，射线AP交ON于点
，且满足且
，请借助图3补全图形，并求
的长．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年北京市昌平区九年级下学期第一次统一练习数学试卷（解析版） 题型：选择题
如图，已知，AB是⊙
的直径，点C，D在⊙上，∠ABC=50°，则∠D为（ ）
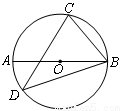
A．50° B．45° C．40° D．30°
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省杭州萧山九校七年级下学期6月质检数学试卷（解析版） 题型：解答题
（本小题满分12分）阅读下列内容，设a，b，c是一个三角形的三条边的长，且a是最长边，我们可以利用a，b，c三边长间的关系来判断这个三角形的形状：
①若
，则该三角形是直角三角形；②若
，则该三角形是钝角三角形；③
，则该三角形是锐角三角形．
例如一个三角形的三边长分别是4，5，6，则最长边是6，由于
，故由上面③可知该三角形是锐角三角形，请解答以下问题：
（1）若一个三角形的三条边长分别是2，3，4，则该三角形是 三角形；
（2）若一个三角形的三条边长分别是3，4，x且这个三角形是直角三角形，则x的值为 ；
（3）若一个三角形的三条边长分别是
，
，
请判断这个三角形的形状，并写出的判断过程．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省杭州萧山九校七年级下学期6月质检数学试卷（解析版） 题型：选择题
观察下列球排列规律●○○ ●○○○○ ●○○ ●○○○○ ●○○●……从第一个到2015个球为止，共有●球（ ）个
A．501 B．502 C．503 D．504
查看答案和解析>>
科目：初中数学 来源：2014-2015学年浙江省杭州萧山九校八年级下学期6月质检数学试卷（解析版） 题型：填空题
为了应对期末考试，老师布置了15道选择题作业，批阅后得到如下统计表，根据表中数据可知，由45名学生答对题数组成的样本的中位数是 ．
查看答案和解析>>
科目：初中数学 来源：2014-2015学年江苏省无锡市八年级5月月检测数学试卷（解析版） 题型：解答题
阅读材料：（本题满分6分）
例：说明代数式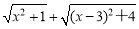 
的几何意义，并求它的最小值．
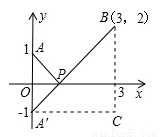
【解析】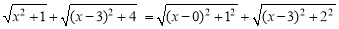
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
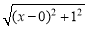可以看成点P与点A（0，1）的距离，
可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C＝3，CB＝3，所以A′B＝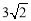
，即原式的最小值为．
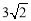根据以上阅读材料，解答下列问题：
（1）代数式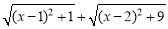
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和．（填写点B的坐标）
（2）代数式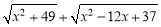 
的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
然后从2，-2，3中任选一个你喜欢的a的值代入求值．
＝ .
，那么分式
的值等于__________．