解:(1)∵AH:AC=2:3,AC=6
∴AH=

AC=

×6=4
又∵HF∥DE,
∴HG∥CB,
∴△AHG∽△ACB
∴
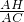
=

,即

=
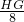
,
∴HG=

∴S
△AHG=

AH•HG=

×4×

=

.
(2)①能为正方形
∵HH′∥CD,HC∥H′D,
∴四边形CDH′H为平行四边形
又∠C=90°,
∴四边形CDH′H为矩形
又CH=AC-AH=6-4=2
∴当CD=CH=2时,四边形CDH′H为正方形
此时可得t=2秒时,四边形CDH′H为正方形.
②(Ⅰ)∵∠DEF=∠ABC,
∴EF∥AB
∴当t=4秒时,直角梯形的腰EF与BA重合.
当0≤t≤4时,重叠部分的面积为直角梯形DEFH′的面积.
过F作FM⊥DE于M,
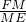
=tan∠DEF=tan∠ABC=

=
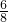
=

∴ME=

FM=

×2=

,HF=DM=DE-ME=4-

=

∴直角梯形DEFH′的面积为

(4+

)×2=

∴y=

.
(Ⅱ)∵当4<t≤5

时,重叠部分的面积为四边形CBGH的面积一矩形CDH′H的面积.
而S
边形CBGH=S
△ABC-S
△AHG=

×8×6-

=

S
矩形CDH′H?=2t
∴y=

-2t.
(Ⅲ)当5

<t≤8时,如图,设H′D交AB于P,
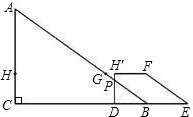
BD=8-t
又
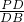
=tan∠ABC=

∴PD=

DB=

(8-t)
∴重叠部分的面积y=S??
△PDB=

PD•DB
=

•

(8-t)(8-t)
=

(8-t)
2=

t
2-6t+24.
∴重叠部分面积y与t的函数关系式:
y=
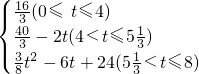
.
分析:(1)由于三角形AHG和ACB相似,可通过相似比求出HG的值,然后根据三角形的面积计算公式即可求出三角形AHG的面积.
(2)①首先四边形CDH′H是个矩形,如果使四边形CDH′H成为正方形,那么需满足的条件是CD=DH′,可先根据AH:AC的值,求出HC的长即H′D的长,然后除以梯形的速度即可求出t的值.
②要分三种情况进行讨论:
一:当E在三角形ABC内部时,即当0≤t≤4时,重合部分是整个直角梯形,因此可通过计算直角梯形的面积得出重合部分的面积.
二:当E在三角形ABC外部,且H′在G点左侧或G点上时,即当4<t≤5

时,重合部分是直角梯形,其面积可用:四边形CBGH的面积一矩形CDH′H的面积来求得.
三:当H′在G点右侧一直到D与B重合的过程中,即当5

<t≤8时,重合部分是个直角三角形.可通过计算这个直角三角形的面积来得出关于S,t的函数关系式.
点评:本题着重考查了图形平移变换、三角形相似以及二次函数的综合应用等重要知识点,
要注意的是(2)中不确定直角梯形的位置时,要根据不同的情况进行分类讨论,不要漏解.


 AC=
AC= ×6=4
×6=4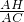 =
= ,即
,即 =
=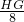 ,
,
 AH•HG=
AH•HG= ×4×
×4× =
= .
.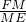 =tan∠DEF=tan∠ABC=
=tan∠DEF=tan∠ABC= =
=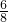 =
=
 FM=
FM= ×2=
×2= ,HF=DM=DE-ME=4-
,HF=DM=DE-ME=4- =
=
 (4+
(4+ )×2=
)×2=
 .
. 时,重叠部分的面积为四边形CBGH的面积一矩形CDH′H的面积.
时,重叠部分的面积为四边形CBGH的面积一矩形CDH′H的面积. ×8×6-
×8×6- =
=
 -2t.
-2t. <t≤8时,如图,设H′D交AB于P,
<t≤8时,如图,设H′D交AB于P, BD=8-t
BD=8-t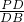 =tan∠ABC=
=tan∠ABC=
 DB=
DB= (8-t)
(8-t) PD•DB
PD•DB •
• (8-t)(8-t)
(8-t)(8-t) (8-t)2=
(8-t)2= t2-6t+24.
t2-6t+24.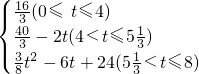 .
. 时,重合部分是直角梯形,其面积可用:四边形CBGH的面积一矩形CDH′H的面积来求得.
时,重合部分是直角梯形,其面积可用:四边形CBGH的面积一矩形CDH′H的面积来求得. <t≤8时,重合部分是个直角三角形.可通过计算这个直角三角形的面积来得出关于S,t的函数关系式.
<t≤8时,重合部分是个直角三角形.可通过计算这个直角三角形的面积来得出关于S,t的函数关系式.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为