
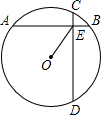
 如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16
如图,半径为12的⊙O中,弦AB与弦CD垂直相交于点E,若AB=16 ,CD=6
,CD=6 ,则OE的长为________.
,则OE的长为________.
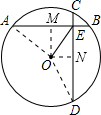 解:过O作OM⊥AB,ON⊥CD,连接OA,OD,
解:过O作OM⊥AB,ON⊥CD,连接OA,OD, ,CD=6
,CD=6 ,
, ,CN=ND=3
,CN=ND=3 ,
, =6,ON=
=6,ON=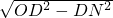 =3,
=3,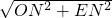 =3
=3 .
.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
 (2012•南关区模拟)如图,半径为6的圆分成12个全等的扇形,并把其中6个涂上阴影.已知∠AOB=120°,在⊙0的转动过程中,阴影部分落在扇形AOB内部的面积为
(2012•南关区模拟)如图,半径为6的圆分成12个全等的扇形,并把其中6个涂上阴影.已知∠AOB=120°,在⊙0的转动过程中,阴影部分落在扇形AOB内部的面积为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com