点A(4,m),B(n,-3)在直线y=x-5上.
(1)试求点A、点B坐标;
(2)若一抛物线过A,B且以y轴为对称轴,求该抛物线解析式;
(3)现有一开口向下,形状与(2)中抛物线相同的新抛物线沿x轴水平移动,交x轴于C,D两点(C左D右),且CD=3.试求当四边形ABCD周长最小时的新抛物线的解析式.
分析:(1)把A,B坐标代入直线解析式即可;
(2)设出函数解析式,把A、B坐标代入;
(3)易得新抛物线的二次项系数与原抛物线的二次项系数互为相反数.四边形ABCD的周长最小,应把已知的一个点平移3个单位,作出另一的点关于x轴的对称点,连接两个新点得到D坐标,进而求得C坐标,代入所设的两个函数解析式即可.
解答:解:(1)∵点A(4,m),B(n,-3)在直线y=x-5上,
∴m=4-5=-1,n=-3+5=2,
A(4,-1),B(2,-3).
(2)设所求函数解析式为y=ax
2+k,
那么-1=16a+k,
-3=4a+k,
解得a=
,b=-
,
∴
y=x2-.
(3)点B向右平移3个单位得E(5,3),作A关于x轴的对称点F(4,1),直线EF与x轴的交点即D
(,0),
再得C为
(,0).
设y=-
x
2+bx+c,
把C,D坐标代入,
可得
y=-x2+x-.
点评:以y轴为对称轴的函数解析式为y=ax2+k两个函数的形状相同,开口方向不同,这两个函数二次项的系数互为相反数;
求路线最短问题,应想到做其中一点的关于另两点所在直线的对称点.



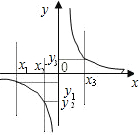 在函数y=
在函数y= 9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为
9、如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),则点A2008的坐标为 23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
23、如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.