
 已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.
已知在平面直角坐标系xOy中(如图),已知抛物线y=-x2+bx+c经过点A(2,2),对称轴是直线x=1,顶点为B.分析 (1)依据抛物线的对称轴方程可求得b的值,然后将点A的坐标代入y=-x2+2x+c可求得c的值;
(2)过点A作AC⊥BM,垂足为C,从而可得到AC=1,MC=m-2,最后利用锐角三角函数的定义求解即可;
(3)由平移后抛物线的顶点在x轴上可求得平移的方向和距离,故此QP=3,然后由点QO=PO,QP∥y轴可得到点Q和P关于x对称,可求得点Q的纵坐标,将点Q的纵坐标代入平移后的解析式可求得对应的x的值,则可得到点Q的坐标.
解答 解:(1)∵抛物线的对称轴为x=1,
∴x=-$\frac{b}{2a}$=1,即$\frac{-b}{2×(-1)}$=1,解得b=2.
∴y=-x2+2x+c.
将A(2,2)代入得:-4+4+c=2,解得:c=2.
∴抛物线的解析式为y=-x2+2x+2.
配方得:y=-(x-1)2+3.
∴抛物线的顶点坐标为(1,3).
(2)如图所示:过点A作AC⊥BM,垂足为C,则AC=1,C(1,2).
∵M(1,m),C(1,2),
∴MC=m-2.
∴cot∠AMB=$\frac{CM}{AC}$=m-2.
(3)∵抛物线的顶点坐标为(1,3),平移后抛物线的顶点坐标在x轴上,
∴抛物线向下平移了3个单位.
∴平移后抛物线的解析式为y=-x2+2x-1,PQ=3.
∵OP=OQ,
∴点O在PQ的垂直平分线上.
又∵QP∥y轴,
∴点Q与点P关于x轴对称.
∴点Q的纵坐标为-$\frac{3}{2}$.
将y=-$\frac{3}{2}$代入y=-x2+2x-1得:-x2+2x-1=-$\frac{3}{2}$,解得:x=$\frac{2+\sqrt{6}}{2}$或x=$\frac{2-\sqrt{6}}{2}$.
∴点Q的坐标为($\frac{2+\sqrt{6}}{2}$,-$\frac{3}{2}$)或($\frac{2-\sqrt{6}}{2}$,-$\frac{3}{2}$).
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义、二次函数的平移规律、线段垂直平分线的性质,发现点Q与点P关于x轴对称,从而得到点Q的纵坐标是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
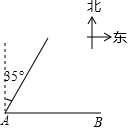 如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )
如图,码头A在码头B的正西方向,甲、乙两船分别从A,B同时出发,并以等速驶向某海域,甲的航向是北偏东35°,为避免行进中甲、乙相撞,则乙的航向不能是( )| A. | 北偏东55° | B. | 北偏西55° | C. | 北偏东35° | D. | 北偏西35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
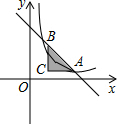 如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.
如图,过C(2,1)作AC∥x轴,BC∥y轴,点A,B都在直线y=-x+6上,若双曲线y=$\frac{k}{x}$(x>0)与△ABC总有公共点,则k的取值范围是2≤k≤9.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
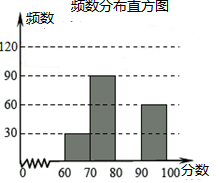 某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
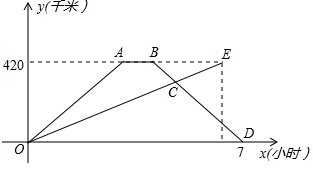 快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )
快车与慢车分别从相距420千米的甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1小时,然后按原路原速返回,快车比慢车晚1小时到达甲地,快慢两车距各自出发地的路程y(千米)与所用的时间x(时)的关系如图所示,下列说法错误的是( )| A. | 快车返回的速度为140千米/时 | |
| B. | 慢车的速度为70千米/时 | |
| C. | 快慢两车出发4$\frac{1}{2}$小时时两车相遇 | |
| D. | 出发$\frac{14}{3}$小时时,快慢两车距各自出发地的路程相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
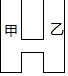 如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )| A. |  | B. | 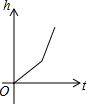 | C. | 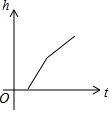 | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com