
【题目】某县为落实“精准扶贫惠民政策”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合作施工15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙两队合作完成.则甲、乙两队合作完成该工程需要多少天?
科目:初中数学 来源: 题型:
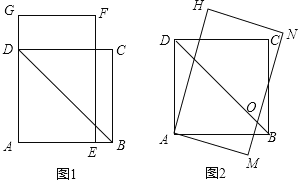
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
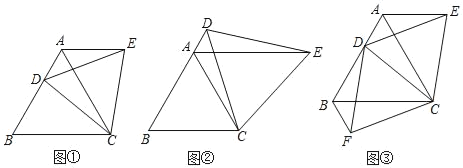
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
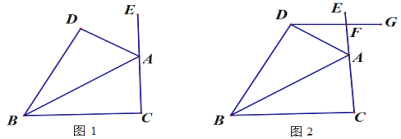
【题目】已知:如图,AB平分∠CBD,∠DBC=60°,∠C=∠D.
(1)若AC⊥BC,求∠BAE的度数;
(2)请探究∠DAE与∠C的数量关系,写出你的探究结论,并加以证明;
(3)如图,过点D作DG∥BC交CE于点F,当∠EFG=2∠DAE时,求∠BAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年巴西里约奥运会期间,南京某奥运特许经营商店以每件
年巴西里约奥运会期间,南京某奥运特许经营商店以每件![]() 元的价格购进了一批奥运纪念
元的价格购进了一批奥运纪念![]() 恤,定价为
恤,定价为![]() 元时,平均每天可售出
元时,平均每天可售出![]() 件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念
件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念![]() 恤的单价每降
恤的单价每降![]() 元,每天可多售出
元,每天可多售出![]() 件.当这种奥运纪念
件.当这种奥运纪念![]() 恤每件的价格定为多少元时,商店每天获利
恤每件的价格定为多少元时,商店每天获利![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列5个结论:①abc<0;②b<a﹣c;③4a+2b+c>0;④2c<3b;⑤a+b<m(am+b),(m≠1的实数)⑥2a+b+c>0,其中正确的结论的有( )
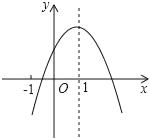
A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
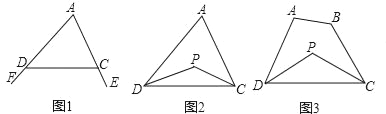
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?
已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com