
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A的坐标为(﹣1,1),点B在x轴正半轴上,点D在第三象限的双曲线y=![]() 上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
上,过点C作CE∥x轴交双曲线于点E,连接BE,则△BCE的面积为( )
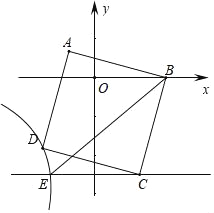
A. 5B. 6C. 7D. 8
【答案】C
【解析】
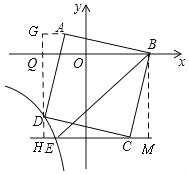
作辅助线,构建全等三角形:过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,证明△AGD≌△DHC≌△CMB,根据点D的坐标表示:AG=DH=-x-1,由DG=BM,列方程可得x的值,表示D和E的坐标,根据三角形面积公式可得结论.
解:过D作GH⊥x轴,过A作AG⊥GH,过B作BM⊥HC于M,
设D(x,![]() ),
),
∵四边形ABCD是正方形,
∴AD=CD=BC,∠ADC=∠DCB=90°,
易得△AGD≌△DHC≌△CMB(AAS),
∴AG=DH=﹣x﹣1,
∴DG=BM,
∵GQ=1,DQ=﹣![]() ,DH=AG=﹣x﹣1,
,DH=AG=﹣x﹣1,
由QG+DQ=BM=DQ+DH得:1﹣![]() =﹣1﹣x﹣
=﹣1﹣x﹣![]() ,
,
解得x=﹣2,
∴D(﹣2,﹣3),CH=DG=BM=1﹣![]() =4,
=4,
∵AG=DH=﹣1﹣x=1,
∴点E的纵坐标为﹣4,
当y=﹣4时,x=﹣![]() ,
,
∴E(﹣![]() ,﹣4),
,﹣4),
∴EH=2﹣![]() =
=![]() ,
,
∴CE=CH﹣HE=4﹣![]() =
=![]() ,
,
∴S△CEB=![]() CEBM=
CEBM=![]() ×
×![]() ×4=7;
×4=7;
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
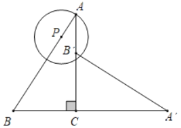
【题目】如图,△ABC中,∠ACB=90°,BC=3,cos∠B=![]() ,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
,将△ABC绕点C顺时针旋转90°得到△AB'C,P为线段AB上的动点,以点P为圆心,PA长为半径作⊙P,当⊙P与△A′B′C的一边所在的直线相切时,⊙P的半径为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,E、F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交AD于点M,交BA的延长线于点Q.连接BM,下列结论中:①AE=BF; ②AE⊥BF;③AQ=![]() ;④∠MBF=60°.
;④∠MBF=60°.
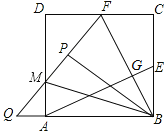
正确的结论是_____(填正确结论的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+c的图象与x轴交于A(﹣3,0)、B(1,0)两点,与y轴交于点C,且OC=OA.
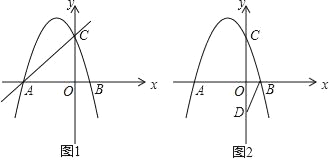
(1)求抛物线解析式;
(2)过直线AC上方的抛物线上一点M作y轴的平行线,与直线AC交于点N.已知M点的横坐标为m,试用含m的式子表示MN的长及△ACM的面积S,并求当MN的长最大时S的值;
(3)如图2,D(0,﹣2),连接BD,将△OBD绕平面内的某点(记为P)逆时针旋转180°得到△O′B′D′,O、B、D的对应点分别为O′、B′、D′.若点B′、D′两点恰好落在抛物线上,求旋转中心点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
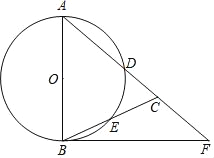
【题目】如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交AC、BC于点D、E,点F在AC的延长线上,且∠A=2∠CBF.
(1)求证:BF与⊙O相切.
(2)若BC=CF=4,求BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
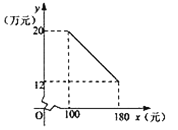
【题目】某科技公司用480万元购得某种产品的生产技术后,并进一步投入资金1520万元购买生产设备,进行该产品的生产加工.已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价不低于100元,但不超过180元.设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元),该产品年销售量
(万元),该产品年销售量![]() (万件)与产品售价
(万件)与产品售价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
(1)求![]() 与
与![]() 之间的函数表达式,并写出
之间的函数表达式,并写出![]() 的取值范围;
的取值范围;
(2)求第一年的年获利![]() 与
与![]() 之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
之间的函数表达式,并说明投资的第一年,该公司是盈利还是亏损?并求当盈利最大或亏损最小时的产品售价;
(3)在(2)的条件下.即在盈利最大或亏损最小时,第二年公司重新确定产品售价,能否使两年共盈利不低于1370万元?若能,求出第二年的售价在什么范围内;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了弘扬我国古代数学发展的伟大成就,某校九年级进行了一次数学知识竞赛,并设立了以我国古代数学家名字命名的四个奖项:“祖冲之奖”、“刘徽奖”、“赵爽奖”和“杨辉奖”,根据获奖情况绘制成如图1和图2所示的条形统计图和扇形统计图,并得到了获“祖冲之奖”的学生成绩统计表:
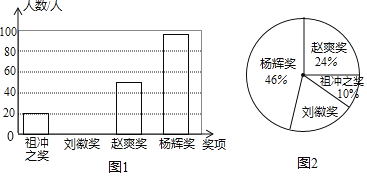
“祖冲之奖”的学生成绩统计表:
分数 | 80 | 85 | 90 | 95 |
人数 | 4 | 2 | 10 | 4 |
根据图表中的信息,解答下列问题:
![]() 这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
这次获得“刘徽奖”的人数是多少,并将条形统计图补充完整;
![]() 获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
获得“祖冲之奖”的学生成绩的中位数是多少分,众数是多少分;
![]() 在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“
在这次数学知识竟赛中有这样一道题:一个不透明的盒子里有完全相同的三个小球,球上分别标有数字“![]() ”,“
”,“![]() ”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点
”和“2”,随机摸出一个小球,把小球上的数字记为x放回后再随机摸出一个小球,把小球上的数字记为y,把x作为横坐标,把y作为纵坐标,记作点![]() 用列表法或树状图法求这个点在第二象限的概率.
用列表法或树状图法求这个点在第二象限的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com