
| A. | a≤1 | B. | -1≤a≤1 | C. | a≤-1 | D. | -1≤a≤0 |
分析 先求出x的值为$\frac{(1-a)^{2}}{4}$,代入已知后变形为$\sqrt{\frac{(1+a)^{2}}{4}}$-$\sqrt{\frac{(3-a)^{2}}{4}}$=-2,开方得:|1+a|-|3-a|=-4,分三种情况进行讨论,a≤-1,-1<a≤3,a>3,分别解方程即可.
解答 解:∵$\sqrt{x}$=$\frac{1-a}{2}$,
∴x=$\frac{(1-a)^{2}}{4}$,
把x=$\frac{(1-a)^{2}}{4}$代入$\sqrt{x+a}$-$\sqrt{x-a+2}$=-2得:
$\sqrt{\frac{(1+a)^{2}}{4}}$-$\sqrt{\frac{(1-a)^{2}}{4}-a+2}$=-2,
$\sqrt{\frac{(1+a)^{2}}{4}}$-$\sqrt{\frac{(3-a)^{2}}{4}}$=-2,
$\frac{|1+a|}{2}-\frac{|3-a|}{2}$=-2,
|1+a|-|3-a|=-4,
分三种情况:
①当a≤-1时,-1-a-(3-a)=-4,
-1-a-3+a=-4,
∴当a≤-1时,都是方程的解;
②当-1<a≤3时,1+a-(3-a)=-4,
1+a-3+a=-4,
a=-1,
此方程无解;
③当a>3时,1+a-(a-3)=-4,
1+a-a+3=-4,
此方程无解;
综上所述,a的取值范围是a≤-1;
故选C.
点评 本题考查了二次根式的加减法和二次根式的意义,根据将已知等式两边同时平方进行变形,并将根号化去,将无理方程化为整式方程,再利用绝对值的意义求解.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
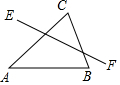 如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )
如图,点D是△ABC中AB边上的一个动点,点D关于AC,BC对称点分别是点E和点F,∠A=45°,∠B=75°,AC=8,则EF的最小值是( )| A. | 4$\sqrt{6}$ | B. | 8 | C. | 4$\sqrt{3}$ | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0是最小的自然数,最大的负数是-1 | |
| B. | 绝对值等于它本身的数是0和1 | |
| C. | 任何有理数的绝对值都是正数 | |
| D. | 任何有理数的绝对值都不可能小于0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com