
| c |
| 3 |
| c |
| 3 |


科目:初中数学 来源: 题型:
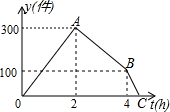 某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有
某种产品从生产流水线上下线后,需要包装人库,通常的办法是,流水线先工作一段时间,包装工人再开始工作.某次包装工人工作一段时间后,因临近下班,又抽调了一部分工人来帮忙,使包装人库的速度提高了一倍.如图是下线后待包装人库的产品数量y(件)与流水线开始工作时间t(h)的函数关系的图象.以下结论正确的有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com