
【题目】如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD= .
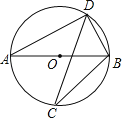
【答案】32°
【解析】
试题分析:根据圆周角定理求得∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半)、∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);根据平角是180°知∠BOD=180°﹣∠AOD,故∠BCD=32°.
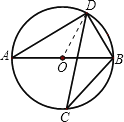
解:连接OD.
∵AB是⊙0的直径,CD是⊙O的弦,∠ABD=58°,
∴∠AOD=2∠ABD=116°(同弧所对的圆周角是所对的圆心角的一半);
又∵∠BOD=180°﹣∠AOD,∠BOD=2∠BCD(同弧所对的圆周角是所对的圆心角的一半);
∴∠BCD=32°;
另法:∵AB为直径,
∴∠ADB=90°,
∵∠ABD=58°,
∴∠A=90°﹣58°=32°,
∵∠BCD和∠A都是BD所对圆周角,
∴∠BCD=32°.
故答案为:32°.


科目:初中数学 来源: 题型:
【题目】几何知识可以解决生活中许多距离最短的问题.让我们从书本一道习题入手进行知识探索.
【回忆】
如图,A、B是河l两侧的两个村庄.现要在河l上修建一个抽水站C,使它到A、B两村庄的距离的和最小,请在图中画出点C的位置,并说明理由.

【探索】
(1)如图,A、B两个村庄在一条笔直的马路的两端,村庄 C在马路外,要在马路上建一个垃圾站O,使得AO+BO+CO最小,请在图中画出点O的位置,并说明理由.

(2)如图,A、B、C、D四个村庄,现建一个垃圾站O,使得AO+BO+CO+DO最小,请在图中画出点O的位置,并说明理由.
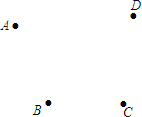
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,3),B(2,4),C(3,5),D(4,6)其中不与E(2,-3)在同一个函数图像上的一个点是( )
A. 点A B. 点B C. 点C D. 点D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. 若|a|=|b|,则a=b B. 若|a|>|b|,则a>b
C. 若a<b|,则|a|<|b| D. 若|a|=|b|,则a=±b
查看答案和解析>>
科目:初中数学 来源: 题型:
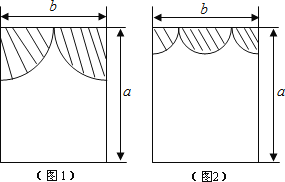
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学学生步行到郊外旅行.高一(1)班学生组成前队,步行速度为4千米/时,高一(2)班学生组成后队,速度为6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知水结成冰的温度是0℃,酒精冻结的温度是–117℃。现有一杯酒精的温度为12℃,放在一个制冷装置里、每分钟温度可降低1.6℃,要使这杯酒精冻结,需要几分钟?(精确到0.1分钟)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com