
����Ŀ����ʵ����ѧѧ�����е��������У���һ��1����ѧ�����ǰ�ӣ������ٶ�Ϊ4ǧ��/ʱ����һ��2����ѧ����ɺ�ӣ��ٶ�Ϊ6ǧ��/ʱ��ǰ�ӳ���1Сʱ��Ӳų�����ͬʱ�����һ������Ա�����г�������֮�䲻��ϵ����ؽ������磬���ﳵ���ٶ�Ϊ12ǧ��/ʱ��
��1�������ǰ����Ҫ�ʱ�䣿
��2�������ǰ��ʱ���ڣ�����Ա�ߵ�·���Ƕ��٣�
��3�����Ӻ�ʱ���2ǧ�ף�
���𰸡���1��2Сʱ����2��24ǧ�ף���3����1Сʱ���3Сʱ���������2ǧ�ף�
��������
�����������1��������ǰ����ҪxСʱ�����ݺ�ӱ�ǰ�ӿ���ٶȡ�ʱ��=ǰ�ӱȺ�����ߵ�·�̿��г����̣�������ɵó�ʱ�䣻
��2���ȼ��������Ա���ߵ�ʱ�䣬����·��=�ٶȡ�ʱ�伴�ɵó�����Ա�ߵ�·�̣�
��3��Ҫ������������ۣ��ٵ���2���û�г�����1����ʱ�����2ǧ�ף��ڵ���2���೬����1�����1�����루2�����ٴ����2ǧ�ף��ֱ��г����̣���⼴�ɣ�
�⣺��1��������ǰ����ҪxСʱ��
��������6��4��x=4��1
��ã�x=2��
�ʺ����ǰ����Ҫ2Сʱ��
��2�������ǰ��ʱ���ڣ�����Ա�ߵ�·�̾�������2Сʱ�����ߵ�·��
����12��2=24
�𣺺����ǰ��ʱ���ڣ�����Ա�ߵ�·����24ǧ�ף�
��3��Ҫ������������ۣ�
�ٵ���1���������Сʱ���������4��![]() =2��ǧ�ף�
=2��ǧ�ף�
�ڵ���2���û�г�����1����ʱ�����2ǧ�ף�
�裨2������yСʱ�루1�����2ǧ�ף�
��������6��4��y=2��
��ã�y=1��
���Ե���2�������1Сʱ���������2ǧ�ף�
�۵���2���೬����1�����1�����루2�����ٴ����2ǧ��ʱ
��6��4��y=4+2��
��ã�y=3
��1Сʱ���3Сʱ���������2ǧ�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�㽭ʡ�����е�7��)�����ε��ڽǺ��ǣ� ��
A��540�� B��720�� C��900�� D��1080��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90����OΪAB��һ�㣬��OΪԲ�ģ�OB��Ϊ�뾶��Բ����BC���ڵ�D����AC�������ڵ�E��
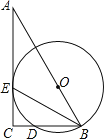
��1����֤��BEƽ����ABC��
��2����CD��BD=1��2��AC=4����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD��BC�ڵ�D��DΪBC���е㣬����AB����ABC��ƽ���߽�AD�ڵ�O������OC������AOC=130��������ABC= ��
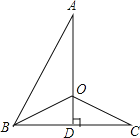
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ����1����x+1��2-x��2-x��������x=2��
��2��-��-2a��3��-b3��2+��ab2��3������a=-1��b=2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l����ԭ��O������x��������ļн�Ϊ30�㣬��M��x���ϣ���M�뾶Ϊ2����M��ֱ��l�ཻ��A��B���㣬����ABMΪ����ֱ�������Σ����M������Ϊ ��
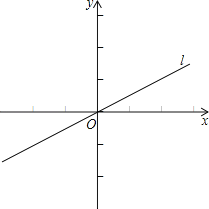
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�ڳ�����ABCD�У�AB=4��BC=![]() ��OΪBC��һ�㣬BO=
��OΪBC��һ�㣬BO=![]() ����ͼ��ʾ����BC����ֱ��Ϊx�ᣬOΪ����ԭ�㽨��ƽ��ֱ������ϵ��MΪ�߶�OC�ϵ�һ�㣮
����ͼ��ʾ����BC����ֱ��Ϊx�ᣬOΪ����ԭ�㽨��ƽ��ֱ������ϵ��MΪ�߶�OC�ϵ�һ�㣮
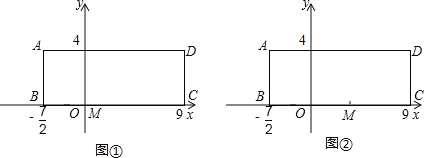
��1������M������Ϊ��1��0������ͼ�٣���OMΪһ����������OMP��ʹ��P��y���ϣ�����������ĵ����������м�������ֱ��д�����з��������ĵ�P�����ꣻ
��2������M������Ϊ��1��0������ͼ�٣���OMΪһ����������OMP��ʹ��P���ڳ�����ABCD��һ���ϣ�����������ĵ����������м�������ֱ��д�����з��������ĵ�P�����꣮
��3��������2���еĵ�M�������Ϊ��4��0���������������䣬��ͼ�ڣ���ô���������ĵ����������м�����������з��������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com