
【题目】如图,Rt△ABC中,∠C=90°,O为AB上一点,以O为圆心,OB长为半径的圆,交BC边于点D,与AC边相切于点E.
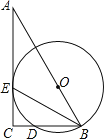
(1)求证:BE平分∠ABC;
(2)若CD:BD=1:2,AC=4,求CD的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)由切线的性质可知OE⊥AC,从而可证明OE∥BC,由平行线的性质可知∠OEB=∠EBC,由OE=OB可知∠OEB=∠OBE,于是得到∠OBE=∠EBC;
(2)过O作OF⊥BC于点F,连接OD,OE.(2)如图2所示:过O作OF⊥BC于点F,连接OD,OE.由等腰三角形三线合一的性质可知:DF=BF,由CD:BD=1:2可知CD=DF=FB,然后根据由三角是直角的四边形为矩形可知四边形OECF为矩形,于是得到CF=EO,从而可证明△ODB为等边三角形,然后依据特殊锐角三角函数值可求得BC=![]() ,故此可求得CD=
,故此可求得CD=![]() .
.
(1)证明:连接OE.
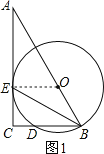
∵OE=OB,
∴∠OEB=∠OBE.
∵AC与⊙O相切,
∴OE⊥AC,即∠OEA=90°.
∴∠C=∠OEA=90°,
∴OE∥BC.
∴∠OEB=∠EBC.
∴∠OBE=∠EBC.
∴BE平分∠ABC.
(2)如图2所示:过O作OF⊥BC于点F,连接OD,OE.
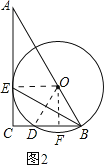
∵OD=OB,OF⊥BD,
∴DF=BF.
∵CD:BD=1:2,
∴CD=DF=FB.
∵∠OEC=∠C=∠OFC=90°,
∴四边形OECF为矩形.
∴CF=EO.
∴OE=BD=OD=OB.
∴△ODB为等边三角形.
∴∠ABC=60°.
∵AC=4,
∴BC=![]() .
.
∴CD=![]() ×BC=
×BC=![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,OB=2OA.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,A(1,3),B(2,4),C(3,5),D(4,6)其中不与E(2,-3)在同一个函数图像上的一个点是( )
A. 点A B. 点B C. 点C D. 点D
查看答案和解析>>
科目:初中数学 来源: 题型:
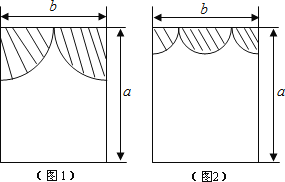
【题目】小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)
(1)用代数式表示窗户能射进阳光的面积是 .(结果保留π)
(2)当![]() ,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
,b=1时,求窗户能射进阳光的面积是多少?(取π≈3)
(3)小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,D是BC的中点,DE⊥AB于点E,若EA=2,则BE=( )
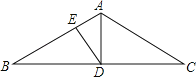
A.3 B.4 C.6 D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市实验中学学生步行到郊外旅行.高一(1)班学生组成前队,步行速度为4千米/时,高一(2)班学生组成后队,速度为6千米/时.前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络,他骑车的速度为12千米/时.
(1)后队追上前队需要多长时间?
(2)后队追上前队时间内,联络员走的路程是多少?
(3)两队何时相距2千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科学家在实验中检测出某微生物约为0.0000035米,将0.0000035用科学记数法表示为( )
A.3.5×10﹣6 B.3.5×106 C.3.5×10﹣5 D.35×10﹣5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com