

分析 (1)根据等边三角形的性质:等边三角形的每一个内角都等于60°,且AM是对称轴进行求解;
(2)根据等边三角形的性质,可以得出AC=AC,DC=EC,∠ACB=∠DCE=60°,由等式的性质得出∠BCE=∠ACD,根据SAS就可以得出△ADC≌△BEC;
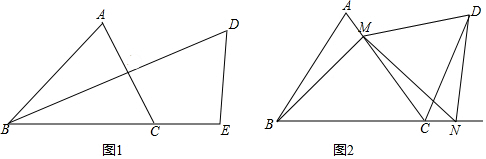
(3)需要分三种情况讨论:当点D在线段AM上时,如图1,由(2)可知△ACD≌△BCE,就可以求出结论;当点D在线段AM的延长线上时,如图2,可以得出△ACD≌△BCE而有∠CBE=∠CAD=30°而得出结论;当点D在线段MA的延长线上时,如图3,通过得出△ACD≌△BCE同样可以得出结论.
解答 解:(1)∵△ABC是等边三角形,
∴∠BAC=60°.
∵AM为△ABC的对称轴,
∴线段AM为BC边上的中线,
∴∠CAM=$\frac{1}{2}$∠BAC,
∴∠CAM=30°.
故答案为:30;
(2)∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠DCB=∠DCB+∠BCE,
∴∠ACD=∠BCE.
在△ADC和△BEC中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ADC≌△BEC(SAS);
(3)∠AOB是定值60°.
理由如下:①当点D在线段AM上时,如图1,
由(2)可知△ACD≌△BCE,则∠CBE=∠CAD=30°,
又∠ABC=60°,
∴∠CBE+∠ABC=60°+30°=90°,
∵∠BAM=∠BAC-∠CAM=30°,
∴∠BOA=90°-30°=60°.
②当点D在线段AM的延长线上时,如图2,
∵△ABC与△DEC都是等边三角形 ,
,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠DCB=∠DCB+∠DCE,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD=30°,
又∵∠BAM=30°,
∴∠BOA=90°-30°=60°.
③当点D在线段MA的延长线上时, 如图3,
如图3,
∵△ABC与△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACD+∠ACE=∠BCE+∠ACE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CBE=∠CAD,
又∵∠CAM=30°,
∴∠CBE=∠CAD=150°,
∴∠CBO=30°,∠BAM=30°,
∴∠BOA=90°-30°=60°.
综上所述,当动点D在直线AM上时,∠AOB是定值,且∠AOB=60°.
点评 本题属于几何变换综合题,主要考查了等边三角形的性质,直角三角形的性质,等式的性质以及全等三角形的判定及性质的综合运用,解答时证明三角形全等是关键.解题时注意:全等三角形的对应角相等;等边三角形的三个内角都相等,且都等于60°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
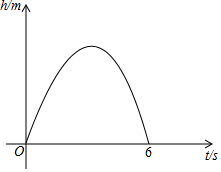 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).
从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 加数的个数n | 连续偶数的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
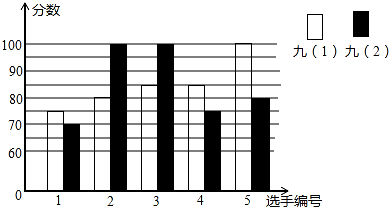 某中学开展某项比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为 100分)如图所示:
某中学开展某项比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为 100分)如图所示:| 班级 | 平均数(分) | 中位数(分) | 众数(分) | 方差 |
| 九(1) | 65 | 85 | 65 | 70 |
| 九(2) | 85 | 80 | 100 | 160 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com