
【题目】已知,m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,抛物线
的两个实数根,且|m|<|n|,抛物线![]() 的图象经过点A(m,0),B(0,n),如图所示.
的图象经过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的解析式;
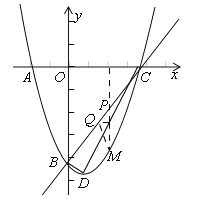
(2)设(1)中的抛物线与x轴的另一个交点为抛物线的顶点为D,试求出点C,D的坐标,并判断△BCD的形状;
(3)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为![]() 个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.

【答案】(1)![]() ;(2)△BCD是直角三角形;(3)S=
;(2)△BCD是直角三角形;(3)S=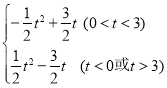 .
.
【解析】
试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;
(2)先解方程求出抛物线与x轴的交点,再判断出△BOC和△BED都是等腰直角三角形,从而得到结论;
(3)先求出QF=1,再分两种情况,当点P在点M上方和下方,分别计算即可.
试题解析:解(1)∵![]() ,∴
,∴![]() ,
,![]() ,∵m,n是一元二次方程
,∵m,n是一元二次方程![]() 的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线
的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线![]() 的图象经过点A(m,0),B(0,n),∴
的图象经过点A(m,0),B(0,n),∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)令y=0,则![]() ,∴
,∴![]() ,
,![]() ,∴C(3,0),∵
,∴C(3,0),∵![]() =
=![]() ,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
,∴顶点坐标D(1,﹣4),过点D作DE⊥y轴,∵OB=OC=3,∴BE=DE=1,∴△BOC和△BED都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD是直角三角形;
(3)如图,∵B(0,﹣3),C(3,0),∴直线BC解析式为y=x﹣3,∵点P的横坐标为t,PM⊥x轴,∴点M的横坐标为t,∵点P在直线BC上,点M在抛物线上,∴P(t,t﹣3),M(t,![]() ),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=
),过点Q作QF⊥PM,∴△PQF是等腰直角三角形,∵PQ=![]() ,∴QF=1.
,∴QF=1.
①当点P在点M上方时,即0<t<3时,PM=t﹣3﹣(![]() )=
)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() =
=![]() ,②如图3,当点P在点M下方时,即t<0或t>3时,PM=
,②如图3,当点P在点M下方时,即t<0或t>3时,PM=![]() ﹣(t﹣3)=
﹣(t﹣3)=![]() ,∴S=
,∴S=![]() PM×QF=
PM×QF=![]() (
(![]() )=
)=![]() .
.
综上所述,S=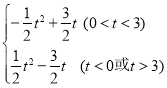 .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() ( a≠0)经过原点,顶点为A ( h,k ) (h≠0).
( a≠0)经过原点,顶点为A ( h,k ) (h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线![]() (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线![]() 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
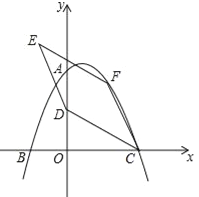
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
的图象与坐标轴交于A、B、C三点,其中点A的坐标为(0,8),点B的坐标为(﹣4,0).
(1)求该二次函数的表达式及点C的坐标;
(2)点D的坐标为(0,4),点F为该二次函数在第一象限内图象上的动点,连接CD、CF,以CD、CF为邻边作平行四边形CDEF,设平行四边形CDEF的面积为S.
①求S的最大值;
②在点F的运动过程中,当点E落在该二次函数图象上时,请直接写出此时S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:
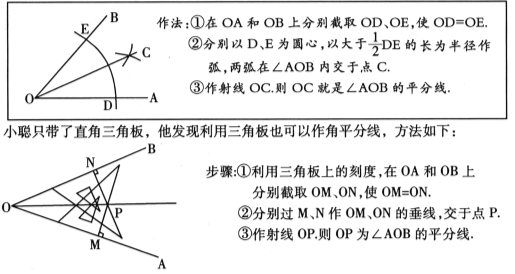
根据以上情境,解决下列问题:
(1)李老师用尺规作角平分线时,用到的三角形全等的判定方法是 .
(2)小聪的作法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当我们利用2种不同的方法计算同一图形的面积时,可以得到一个等式.例如,由图1可得等式:(a+2b)(a+b)=a2+3ab+2b2.
(1)由图2,可得等式:_____________________________
(2)利用(1)中所得到的结论,解决下面的问题:
已知 a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
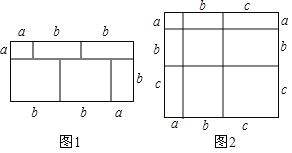
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com