
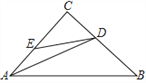
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
【答案】A
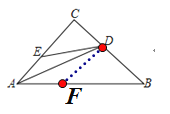
【解析】在AB上截取AF=AE,交AB于点F,如图所示:
∵AD是∠CAB的角平分线,
∴∠EAD=∠FAD,
在△AED和△AFD中,
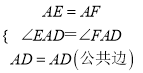 ,
,
∴△AED≌△AFD(SAS),
∴∠DEA=∠DFA,DF=DE,
又∵DE=DB,
∴DF=DB,
∴∠DFB=∠B,
又∵∠DFA+∠DFB=180o,∠DEA=∠DFA,
∴∠DEA+∠B=180°(等量代换),
又∵∠CED+∠AED=180o,
∴∠CED=∠B,
又∵∠C+∠CED+∠CDE=180o,∠C+∠CAB+∠B=180o,
∴∠CDE=∠CAB,
过点D作DG![]() AB于点G,如图所示:
AB于点G,如图所示:
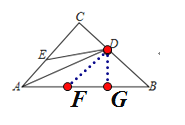
∵DG=DB(已证),
∴DG是BF的垂直平分线,
∴FG=BG,
∵AD是是∠CAB的角平分线,∠C=90°,DG![]() AB,
AB,
∴DC=DG,
在△ADC和△AGD中
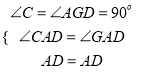 ,
,
∴△ADC≌△AGD(AAS),
∴AC=AG,
又∵AC=AE+CE,AG=AF+FG,
∴AE+CE=AF+FG,
又∵AE=AF,
∴CE=FG,
又∵FG=BG,
∴CE=BG,
∴AC=AE+BG,
又∵AB+AE=AG+BG+AE,AG=AC,
∴AB+AE=AC+AC=2AC,即AC=![]() (AB+AE),
(AB+AE),
∵S四边形ABDE=S△ABD+S△AED=![]() ,
,
∴S四边形ABDE ![]() ,
,
又∵S△ADC=![]() ,
,
∴S△ADC=![]() S四边形ABDE.
S四边形ABDE.
故①②③④都正确,共计4个正确.
故选A.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】一列长150米的火车,以每秒15米的速度通过750米的隧道,从火车进入隧道口算起,这列火车完全通过隧道所需时间是( )
A.70秒
B.60秒
C.50秒
D.40秒
查看答案和解析>>
科目:初中数学 来源: 题型:
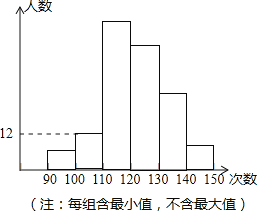
【题目】为了了解合肥市九年级毕业生的体能情况,合肥市随机抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)第二小组的人数占这次抽调学生总数的百分之几?
(2)这次共抽调了多少人?
(3)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是 (在横线上直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
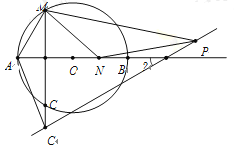
【题目】如图,AB为⊙O的直径,AB=2,点在M在QO上,MC垂直平分OA,点N为直线AB上一动点(N不与A重合),若△MNP∽△MAC,PC与直线AB所夹锐角为α.
(1)若AM=AC,点N与点O重合,则α= °;
(2)若点C、点N的位置如图所示,求α的度数;
(3)当直线PC与⊙O相切时,则MC的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D、E是△ABC内的两点,AE平分∠BAC,∠D=∠DBC=60°,若BD=5cm,DE=3cm,则BC的长是 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在中考体育加试中,某班30名男生的跳远成绩如下表:
成绩/m | 1.95 | 2.00 | 2.05 | 2.10 | 2.15 | 2.25 |
人数 | 2 | 3 | 9 | 8 | 5 | 3 |
这些男生跳远成绩的众数、中位数分别是( )
A. 2.10,2.05B. 2.10,2.10C. 2.05,2.10D. 2.05,2.05
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD.求证:EF=BE+FD;
∠BAD.求证:EF=BE+FD;
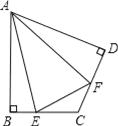
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?
∠BAD,(1)中的结论是否仍然成立?
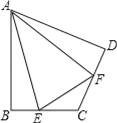
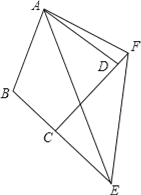
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=![]() ∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com