
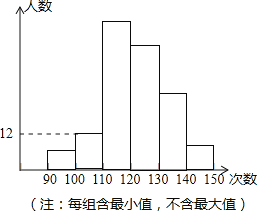
【题目】为了了解合肥市九年级毕业生的体能情况,合肥市随机抽调了一部分学生进行一分钟跳绳测试,将测试成绩整理后作出如图统计图.甲同学计算出前两组的频率和是0.12,乙同学计算出跳绳次数不少于100次的同学占96%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
(1)第二小组的人数占这次抽调学生总数的百分之几?
(2)这次共抽调了多少人?
(3)若跳绳次数不少于130次为优秀,则这次测试成绩的优秀率是 (在横线上直接写出答案).
【答案】(1)8%;(2)150人;(3)24%
【解析】试题分析:(1)根据题意:结合各小组频数之和等于数据总和,各小组频率之和等于1;易得第二组的频率0.08,进而得出第二小组的人数占这次抽调学生总数的百分比;
(2)根据第二组的频率0.08;再由频率、频数的关系频率=![]() ;可得总人数.
;可得总人数.
(3)根据题意:从左至右第二、三、四组的频数比为4:17:15,和(1)的结论;容易求得各组的人数,这样就能求出优秀率.
试题解析:解:(1)∵不少于100次的同学占96%,∴第一组的频率为1﹣0.96=0.04,∵前两组的频率和是0.12,∴第二组的频率为0.12﹣0.04=0.08,∴第二小组的人数占这次抽调学生总数的:0.08×100%=8%;
(2)∵第二组的频率为0.12﹣0.04=0.08,∴故总人数为12÷0.08=150(人),即这次共抽调了150人;
(3)第一组人数为150×0.04=6(人),第三、四组人数分别为51人、45人,这次测试的优秀率为![]() ×100%=24%;
×100%=24%;
故答案为:24%.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1厘米/秒的速度移动,点Q从点B开始沿BC边向点C以2厘米/秒的速度移动。如果P、Q分别是从A、B同时出发,
(1)那么几秒后,△PBQ的面积等于9平方厘米?
(2)那么几秒后,点P与点Q之间的距离可能为5厘米吗?说明理由。
(3)那么几秒后,五边形APQCD的面积最小?最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知代数式:4x﹣4xy+y2﹣x2y3.
①将代数式按照y的次数降幂排列;
②当x=2,y=﹣1时,求该代数式的值.
(2)已知:关于xyz的代数式﹣(m+3)x2y|m+1|z+(2m﹣n)x2y+5为五次二项式,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果2006﹣200.6=x﹣20.06,那么x等于( )
A. 1824.46 B. 1825.46 C. 1826.46 D. 1827.46
查看答案和解析>>
科目:初中数学 来源: 题型:
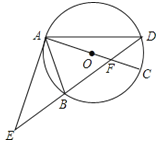
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)已知AF=4,CF=2,在(2)的条件下,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
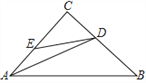
【题目】如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;② ∠CDE=∠CAB;③ AC=![]() (AB+AE);④ S△ADC=
(AB+AE);④ S△ADC=![]() S四边形ABDE,其中正确的结论个数为( )
S四边形ABDE,其中正确的结论个数为( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com