
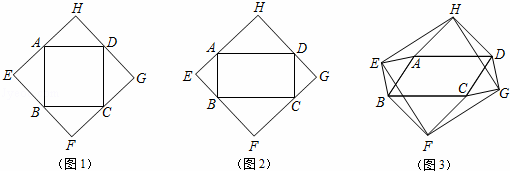
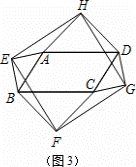
以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
分析: (1)根据等腰直角三角形的性质得到∠E=∠F=∠G=∠H=90°,求出四边形是矩形,根据勾股定理求出AH=HD=![]() AD,DG=GC=
AD,DG=GC=![]() CD,CF=BF=
CD,CF=BF=![]() BC,AE=BE=
BC,AE=BE=![]() AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
(2)①根据平行四边形的性质得出,∠BAD=180°﹣a,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根据△AEB和△DGC是等腰直角三角形,得出AE=![]() AB,DG=
AB,DG=![]() CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;
CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;
③与②证明过程类似求出GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,证△HAE≌△HDG,求出∠AHD=90°,∠EHG=90°,即可推出结论.
解答: (1)解:四边形EFGH的形状是正方形.
(2)解:①∠HAE=90°+a,
在平行四边形ABCD中AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣a,
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣(180°﹣a)=90°+a,
答:用含α的代数式表示∠HAE是90°+a.
②证明:∵△AEB和△DGC是等腰直角三角形,
∴AE=![]() AB,DG=
AB,DG=![]() CD,
CD,
在平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+a=∠HAE,
∵△AHD是等腰直角三角形,
∴HA=HD,
∴△HAE≌△HDG,
∴HE=HG.
③答:四边形EFGH是正方形,
理由是:由②同理可得:GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
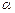 (0°<
(0°<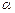 <90°),
<90°),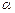 的代数式表示∠HAE= ;(1分)
的代数式表示∠HAE= ;(1分)
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州张家港市第二中学八年级上学期期中考试数学卷 题型:解答题
(本题10分) 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点得四边形EFGH.如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;
【小题1】(1)如图2,当四边形ABCD为矩形时,则四边形EFGH的形状是 ;(1分)
【小题2】(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC= (0°<
(0°< <90°),
<90°),
【小题3】① 试用含 的代数式表示∠HAE= ;(1分)
的代数式表示∠HAE= ;(1分)
【小题4】② 求证:HE=HG;(4分)③ 四边形EFGH是什么四边形?并说明理由.(4分)
查看答案和解析>>
科目:初中数学 来源:2011-2012年江苏省苏州张家港市八年级上学期期中考试数学卷 题型:解答题
(本题10分) 以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连结这四个点得四边形EFGH.如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;
1.(1)如图2,当四边形ABCD为矩形时,则四边形EFGH的形状是 ;(1分)
2.(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC= (0°<
(0°< <90°),
<90°),
3.① 试用含 的代数式表示∠HAE=
;(1分)
的代数式表示∠HAE=
;(1分)
4.② 求证:HE=HG;(4分)③ 四边形EFGH是什么四边形?并说明理由.(4分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com