
【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,下列说法:①∠APE=∠C,②AQ=BQ,③BP=2PQ,④AE+BD=AB,其中正确的个数有( )个。
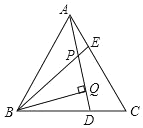
A. 4B. 3C. 2D. 1
【答案】B
【解析】
根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,利用“边角边”证明△ABE和△CAD全等,然后分析判断各选项即可.
证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
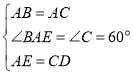 ,
,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∴∠APE=∠C=60°,故①正确
∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.故③正确,
∵AC=BC.AE=DC,
∴BD=CE,
∴AE+BD=AE+EC=AC=AB,故④正确,
无法判断BQ=AQ,故②错误,
故选B.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )

A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
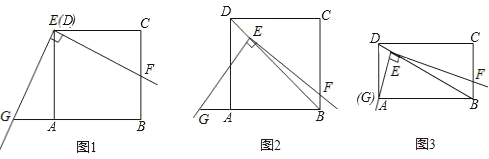
【题目】请你认真阅读下面的小探究系列,完成所提出的问题.
(1)如图1,将角尺放在正方形ABCD上,使角尺的直角顶点E与正方形ABCD的顶点D重合,角尺的一边交CB于点F,将另一边交BA的延长线于点G.求证:EF=EG.
(2)如图2,移动角尺,使角尺的顶点E始终在正方形ABCD的对角线BD上,其余条件不变,请你思考后直接回答EF和EG的数量关系:EF EG(用“=”或“≠”填空)
(3)运用(1)(2)解答中所积累的活动经验和数学知识,完成下题:如图3,将(2)中的“正方形ABCD”改成“矩形ABCD”,使角尺的一边经过点A(即点G、A重合),其余条件不变,若AB=4,BC=3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某木板加工厂将购进的A型、B型两种木板加工成C型,D型两种木板出售,已知一块A型木板的进价比一块B型木板的进价少10元,且购买3块A型木板和2块B型木板共花费120元.
(1)A型木板与B型木板的进价各是多少元?
(2)根据市场需求,该木板加工厂决定用不超过2770元购进A型木板、B型木板共100块,若一块A型木板可制成1块C型木板、2块D型木板;一块B型木板可制成2块C型木板、1块D型木板,且生产出来的C型木板数量不少于D型木板的数量的7/5.
①该木板加工厂有几种进货方案?
②若C型木板每块售价30元,D型木板每块售价25元,且生产出来的C型木板、D型木板全部售出,哪一种方案获得的利润最大,求出最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小乌龟从某点![]() 出发,在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:
出发,在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬行的各段路程依次为(单位:![]() ):+5,-3,+10,-8,-6,+12,-10
):+5,-3,+10,-8,-6,+12,-10
(1)小乌龟最后是否回到出发点![]() ?
?
(2)小乌龟离开原点的距离最远是多少厘米?
(3)小乌龟在爬行过程中,若每爬行![]() 奖励1粒芝麻,则小乌龟一共得到多少粒芝麻?
奖励1粒芝麻,则小乌龟一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() 两点在数轴上,点
两点在数轴上,点![]() 表示的数为-10,
表示的数为-10,![]() ,点
,点![]() 以每秒3个单位长度的速度从点
以每秒3个单位长度的速度从点![]() 向右运动.点
向右运动.点![]() 以每秒2个单位长度的速度从点
以每秒2个单位长度的速度从点![]() 向右运动(点
向右运动(点![]() 、
、![]() 同时出发)
同时出发)
![]()
(1)请你写出数轴上点![]() 对应的数;
对应的数;
(2)当运动的时间为3秒时,请你求出此时点![]() 、
、![]() 在数轴上对应的数,并求出
在数轴上对应的数,并求出![]() 、
、![]() 之间的距离;
之间的距离;
(3)经过几秒,点![]() 、点
、点![]() 分别到原点
分别到原点![]() 的距离相等.
的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮玩扑克牌游戏,小明背对小亮,让小亮按下列四个步骤操作:
第一步:分发左、中、右三堆牌,每堆牌都为![]() 张,且
张,且![]() ;
;
第二步:从左边一堆拿出两张,放入中间一堆;
第三步:从右边一堆拿出五张,放入中间一堆
第四步:左边一堆有几张牌,就从中间一堆拿几张牌放入左边一堆.
(1)填写下表中的空格:
步骤 | 左边一堆牌的张数 | 中间一堆牌的张数 | 右边一堆牌的张数 |
第一步后 |
|
|
|
第二步后 |
|
| |
第三步后 |
|
| |
第四步后 |
|
(2)如若第四步完成后,中间一堆牌的张数的2倍恰好是右边一堆牌的张数的3倍,试求第一步后,每堆牌各有多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校体育组为了解全校学生“最喜欢的一项球类项目”,随机抽取了部分学生进行调查,下面是根据调查结果绘制的不完整的统计图:
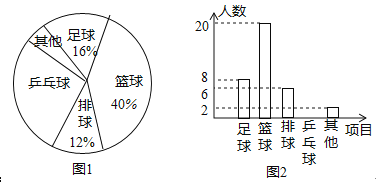
请你根据统计图回答下列问题:
(1)喜欢乒乓球的学生所占的百分比是多少?并请补全条形统计图;
(2)请你估计全校500名学生中最喜欢“排球”项目的有多少名?
(3)在扇形统计图中,“篮球”部分所对应的圆心角是多少度?
(4)篮球教练在制定训练计划前,将从最喜欢篮球项目的甲、乙、丙、丁四名同学中任选两人进行个别座谈,请用列表法或树状图法求抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD中,AC⊥BD于点E,AB=AC=BD,点M为BC中点,N为线段AM上的点,且MB=MN.
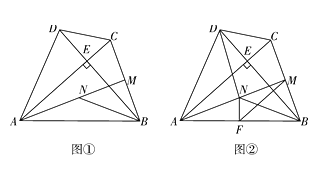
(1)求证:BN平分∠ABE;
(2)若BD=1,连结DN,当四边形DNBC为平行四边形时,求线段BC的长;
(3)如图②,若点F为AB的中点,连结FN、FM,求证:△MFN∽△BDC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com